题目内容
 已知一次函数y=kx+b的图象是直线l,根据图象解答下列问题:
已知一次函数y=kx+b的图象是直线l,根据图象解答下列问题:(1)求k和b的值.
(2)点P(m,1)在直线l上,求点P的坐标.
(3)求不等式kx+b<1的解集.
考点:一次函数与一元一次不等式,一次函数图象上点的坐标特征
专题:计算题
分析:(1)把直线l与坐标的交点坐标代入y=kx+b得到关于k和b的方程组,然后解方程组即可;
(2)把P(m,1)代入得
m+2=1,然后解一次方程即可;
(3)观察函数图象得到,当x<-2时,函数值小于1,从而得到不等式kx+b<1的解集.
(2)把P(m,1)代入得
| 1 |
| 2 |
(3)观察函数图象得到,当x<-2时,函数值小于1,从而得到不等式kx+b<1的解集.
解答:解:(1)把(-4,0)、(0,2)代入y=kx+b得
,解得
;
(2)一次函数解析式为y=
x+2,
把P(m,1)代入得
m+2=1,解得m=-2,
所以P点坐标为(-2,1);
(3)当x<-2时,y<1,则不等式kx+b<1的解集为x<-2.
|
|
(2)一次函数解析式为y=
| 1 |
| 2 |
把P(m,1)代入得
| 1 |
| 2 |
所以P点坐标为(-2,1);
(3)当x<-2时,y<1,则不等式kx+b<1的解集为x<-2.
点评:本题考查了一次函数与一元一次不等式:从函数的角度看,就是寻求使一次函数y=ax+b的值大于(或小于)0的自变量x的取值范围;从函数图象的角度看,就是确定直线y=kx+b在x轴上(或下)方部分所有的点的横坐标所构成的集合.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
方程x(x+4)=x+4的解为( )
| A、x=1 |
| B、x=-4 |
| C、x1=1,x2=-4 |
| D、x1=-1,x2=4 |
 如图.D是AB的中点,DE∥BC,AF⊥BC,垂足为F,AF交DE于G,则AG:AF的值为( )
如图.D是AB的中点,DE∥BC,AF⊥BC,垂足为F,AF交DE于G,则AG:AF的值为( )| A、1:2 | B、1:4 |
| C、2:1 | D、4:1 |
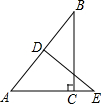 如图,△ABC中,∠ACB=90°,AB=10,BC比AC大2,DE垂直平分AB,交AB于D,交AC的延长线于E.求:
如图,△ABC中,∠ACB=90°,AB=10,BC比AC大2,DE垂直平分AB,交AB于D,交AC的延长线于E.求: 已知∠ABM=90°,AB=AC,过点A作AG丄BC,垂足为G,延长AG交BM于点,过点A作AN∥BM,过点C作EF∥AD,与射线AN、BM分别相交于点F、E
已知∠ABM=90°,AB=AC,过点A作AG丄BC,垂足为G,延长AG交BM于点,过点A作AN∥BM,过点C作EF∥AD,与射线AN、BM分别相交于点F、E  如图,A、B对应的数为-1,-
如图,A、B对应的数为-1,- 如图,矩形ABCD的对角线相交于点O,BE⊥AC于点E,EB的延长线与∠ADC的角平线相交于点F,DF交AC于点M,求证:AC=BF.
如图,矩形ABCD的对角线相交于点O,BE⊥AC于点E,EB的延长线与∠ADC的角平线相交于点F,DF交AC于点M,求证:AC=BF.