题目内容
3.直角三角形两直角边分别是30cm和40cm,则斜边上的中线长为25cm.分析 根据勾股定理求出斜边长,根据直角三角形的性质计算即可.
解答 解:由勾股定理得,斜边长=$\sqrt{3{0}^{2}+4{0}^{2}}$=50cm,
∴斜边上的中线长=$\frac{1}{2}$×50=25cm,
故答案为:25.
点评 本题考查的是勾股定理的应用以及直角三角形的性质,直角三角形的两条直角边长分别是a,b,斜边长为c,那么a2+b2=c2.

练习册系列答案
相关题目
18.下列四个多项式中,含有因式x-1的是( )
| A. | 2x-1 | B. | -4xy+4x | C. | x2-2x+1 | D. | x2-4 |
12.某校计划修建一座既是中心对称图形又是轴对称图形的花坛,从学生中征集到设计方案有等腰三角形、正三角形、平行四边形、菱形等四种图案,你认为符合条件的是( )
| A. | 等腰三角形 | B. | 正三角形 | C. | 平行四边形 | D. | 菱形 |
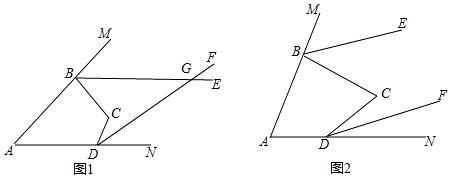
 如图,点C是线段AB上一点,点M,N,P分别是线段AC,BC,AB的中点.
如图,点C是线段AB上一点,点M,N,P分别是线段AC,BC,AB的中点. 如图,折线ABC是在某市乘出租车所付车费y(元)与行车里程x(km)之间的函数关系图象.
如图,折线ABC是在某市乘出租车所付车费y(元)与行车里程x(km)之间的函数关系图象.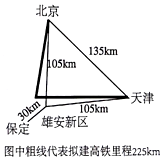 “雄安新区”是中共中央作出“千年大计、国家大事”的重大决策,雄安新区位于北京、天津和保定构成的一个等边三角形腹地,距离北京、天津和保定市分别约105公里、105公里、30公里,如图所示.现拟一列高铁列车从北京经雄安新区到天津比北京与天津的城际特快列车还少用25分,已知高铁速度是城际特快列车的速度2.5倍,高铁列车行驶的里程为225km,北京与天津的里程为135km,求城际特快列车的速度是多少km/h?
“雄安新区”是中共中央作出“千年大计、国家大事”的重大决策,雄安新区位于北京、天津和保定构成的一个等边三角形腹地,距离北京、天津和保定市分别约105公里、105公里、30公里,如图所示.现拟一列高铁列车从北京经雄安新区到天津比北京与天津的城际特快列车还少用25分,已知高铁速度是城际特快列车的速度2.5倍,高铁列车行驶的里程为225km,北京与天津的里程为135km,求城际特快列车的速度是多少km/h?