题目内容
5.函数y=kx+2k+1,(1)当-1≤x≤1时,函数f(x)的值有正也有负,求k的取值范围;
(2)当-1≤x≤1时,函数f(x)的值恒为负,求k的取值范围;
(3)当-1≤x≤1时,函数f(x)的值恒为正,求k的取值范围.
分析 (1)由题意,当-1≤x≤1时,y的值有正也有负,即f(-1)•f(1)<0,代入求出k的取值范围;
(2)由题意,当-1≤x≤1时,y的值恒为负,即f(-1)<0,且f(1)<0,代入求出k的取值范围;
(3)由题意,当-1≤x≤1时,y的值恒为正,即f(-1)>0,且f(1)>0,代入求出k的取值范围.
解答 解:(1)∵y=f(x)=kx+2k+1,当-1≤x≤1时,y的值有正也有负,
∴f(-1)•f(1)<0,
即(-k+2k+1)•(k+2k+1)<0,
∴(k+1)•(3k+1)<0
解得-1<k<-$\frac{1}{3}$;
∴k的取值范围是{k|-1<k<-$\frac{1}{3}$};
(2)∵y=f(x)=kx+2k+1,当-1≤x≤1时,y的值恒为负,
∴f(-1)<0,且f(1)<0,
即(-k+2k+1)<0,(k+2k+1)<0,
∴(k+1)•(3k+1)>0
解得k<-1;
∴k的取值范围是k<-1;
(3)∵y=f(x)=kx+2k+1,当-1≤x≤1时,y的值恒为正,
∴f(-1)>0,且f(1)>0,
即(-k+2k+1)•(k+2k+1)>0,
∴(k+1)•(3k+1)>0
解得k>-$\frac{1}{3}$;
∴k的取值范围是k>-$\frac{1}{3}$.
点评 本题考查了一次函数的图象与性质,解题时结合图形,容易解得答案,是基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,在△AEC中,点D是EC上的一点,且AE=AD,AB=AC,∠1=∠2.求证:BD=EC.
如图,在△AEC中,点D是EC上的一点,且AE=AD,AB=AC,∠1=∠2.求证:BD=EC. 如图,四边形ABCD是边长为a的正方形,点G、E分别是边AB、BC的中点,∠AEF=90°,且EF交正方形外角的平方线CF于点F.
如图,四边形ABCD是边长为a的正方形,点G、E分别是边AB、BC的中点,∠AEF=90°,且EF交正方形外角的平方线CF于点F.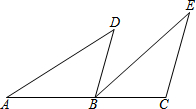 已知:如图,点A、B、C在一条直线上,BD∥CE,AB=EC,BD=CB.
已知:如图,点A、B、C在一条直线上,BD∥CE,AB=EC,BD=CB. 有理数a、b、c在数轴上的位置如图所示,求|a|、|-b|和-|-c|的值.
有理数a、b、c在数轴上的位置如图所示,求|a|、|-b|和-|-c|的值. 已知函数y=-x2+bx+2b-1的部分图象如图所示,求函数的解析式.
已知函数y=-x2+bx+2b-1的部分图象如图所示,求函数的解析式.