题目内容
14.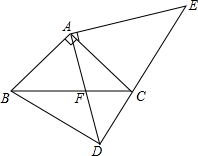 如图,在△ABC和△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C、D、E在同一直线上,连结BD.
如图,在△ABC和△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C、D、E在同一直线上,连结BD.(1)求证:BD=EC;
(2)BD与CE有何位置关系?请证你的猜想.
分析 (1)求出∠BAD=∠CAE,根据SAS推出△ABD≌△ACE,根据全等三角形的性质推出即可;
(2)根据全等三角形的性质得出∠BDA=∠E,根据∠E+∠ADE=90°求出∠BDA+∠ADE=90°即可.
解答 (1)证明:∵∠BAC=∠DAE=90°,
∴∠BAC-∠DAC=∠DAE-∠DAC,
即∠BAD=∠CAE,
在△ABD和△ACE中,
$\left\{\begin{array}{l}{AB=AC}\\{∠BAD=∠CAE}\\{AD=AE}\end{array}\right.$,
∴△ABD≌△ACE(SAS),
∴BD=EC;
(2)BD⊥CE,
证明:∵△ABD≌△ACE,
∴∠BDA=∠E,
又∵∠E+∠ADE=90°,
∴∠BDA+∠ADE=90°,即∠BDE=90°,
∴BD⊥DE.
点评 本题考查了全等三角形的性质和判定的应用,能综合运用定理进行推理是解此题的关键,注意:①全等三角形的判定定理有SAS,ASA,AAS,SSS,②全等三角形的对应角相等,对应边相等.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
19.正方体的截面中,边数最多的多边形是( )
| A. | 四边形 | B. | 五边形 | C. | 六边形 | D. | 七边形 |
6.用四舍五入法,把数4.803保留三个有效数字,得到的近似数是( )
| A. | 4.8 | B. | 4.80 | C. | 4.803 | D. | 5.0 |
3.下列命题中,正确的是( )
| A. | 形状相同的两个三角形是全等形 | B. | 面积相等的两个三角形全等 | ||
| C. | 周长相等的两个三角形全等 | D. | 周长相等的两个等边三角形全等 |
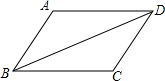 如图所示,BD是四边形ABCD的对角线,AD∥CB,请添加一个条件,使△ABD≌△CDB,这个添加的条件可以是AD=CB.(只需填一个,不添加辅助线)
如图所示,BD是四边形ABCD的对角线,AD∥CB,请添加一个条件,使△ABD≌△CDB,这个添加的条件可以是AD=CB.(只需填一个,不添加辅助线) 如图,PA、PB切⊙O于A、B两点,CD切⊙O于点E,交PA、PB于C、D.若⊙O的半径为2,△PCD的周长等于6,则OP=$\sqrt{13}$.
如图,PA、PB切⊙O于A、B两点,CD切⊙O于点E,交PA、PB于C、D.若⊙O的半径为2,△PCD的周长等于6,则OP=$\sqrt{13}$. 如图,已知△ABC的三个顶点的坐标分别为A(-2,3)、B(-6,0)、C(-1,0).
如图,已知△ABC的三个顶点的坐标分别为A(-2,3)、B(-6,0)、C(-1,0).