题目内容
4.如图,抛物线y=$\frac{1}{2}$x2+bx+c与x轴相交于点A(-1,0)、B(3,0),直线y=kx+1与抛物线相交于A、C两点(1)求抛物线y=$\frac{1}{2}$x2+bx+c和直线AC的解析式;
(2)以AC为直径的圆与y轴交于两点M、N,求M、N两点的坐标;
(3)在抛物线的对称轴上是否存在一点P,△ACP的内心也在对称轴上,若存在,求点P的坐标;若不存在,说明理由.
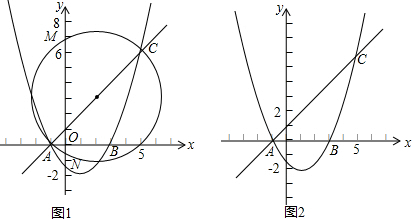
分析 (1)根据待定系数法求得即可;
(2)联立方程求得C点的坐标,进而求得圆心D的坐标,然后根据垂径定理和勾股定理即可求得;
(3)求得抛物线的对称轴,然后作CG⊥y轴,交对称轴与G,设对称轴与x轴交于H,由题意可知∠APH=∠CPG,从而证得△APH∽△CPG,得出$\frac{AH}{PH}$=$\frac{CG}{PG}$,设P的坐标为(1,a),则AH=2,PH=-a,CG=4,PG=6-a,根据相似三角形对应边成比例即可求得a的值.
解答 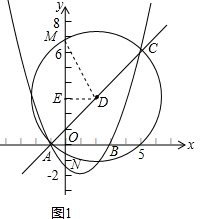 解:(1)∵抛物线y=$\frac{1}{2}$x2+bx+c与x轴相交于点A(-1,0)、B(3,0),
解:(1)∵抛物线y=$\frac{1}{2}$x2+bx+c与x轴相交于点A(-1,0)、B(3,0),
∴$\left\{\begin{array}{l}{\frac{1}{2}-b+c=0}\\{\frac{9}{2}+3b+c=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{b=-1}\\{c=-\frac{3}{2}}\end{array}\right.$,
∴抛物线的解析式为$y=\frac{1}{2}{x^2}-x-\frac{3}{2}$,
∵直线y=kx+1经过点A(-1,0),
∴-k+1=0,解得k=1,
∴直线AC的解析式为y=x+1;
(2)解$\left\{\begin{array}{l}{y=x+1}\\{y=\frac{1}{2}{x}^{2}-x-\frac{3}{2}}\end{array}\right.$得$\left\{\begin{array}{l}{x=-1}\\{y=0}\end{array}\right.$或$\left\{\begin{array}{l}{x=5}\\{y=6}\end{array}\right.$,
∴A(-1,0),C(5,6),
∴圆心D的坐标为(2,3),AC=$\sqrt{(5+1)^{2}+{6}^{2}}$=6$\sqrt{2}$,
作DE⊥y轴于E,则DE=2,连接DM,则DM=3$\sqrt{2}$,
∴EM=$\sqrt{D{M}^{2}-D{E}^{2}}$=$\sqrt{14}$,
∴M(0,3+$\sqrt{14}$),N(0,3-$\sqrt{14}$)
(3)作CG⊥y轴,交对称轴与G,设对称轴与x轴交于H,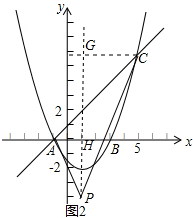
由题意可知∠APH=∠CPG,
∴△APH∽△CPG,
∴$\frac{AH}{PH}$=$\frac{CG}{PG}$,
∵抛物线的解析式为$y=\frac{1}{2}{x^2}-x-\frac{3}{2}$=$\frac{1}{2}$(x-1)2-2
∴抛物线的对称轴为x=1,
设P的坐标为(1,a),
∴AH=2,PH=-a,CG=4,PG=6-a,
∴$\frac{2}{-a}$=$\frac{4}{6-a}$,解得a=-6,
∴P(1,-6).
点评 本题是二次函数的综合题,考查了待定系数法求二次函数和一次函数的解析式,垂径定理和勾股定理的应用,三角形相似的判定和性质,(3)根据内心的性质得出∠APH=∠CPG是解题的关键.

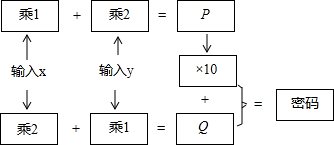 如图是一个密码产生程序,输入数字x、y(1~9)后进行若干步计算分别得到P和Q,再由10P+Q的值确定一个密码,如果要产生密码96,那么x=1,y=4.
如图是一个密码产生程序,输入数字x、y(1~9)后进行若干步计算分别得到P和Q,再由10P+Q的值确定一个密码,如果要产生密码96,那么x=1,y=4.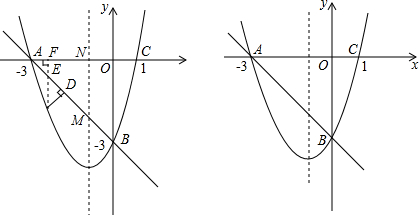
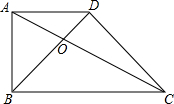 如图,已知梯形ABCD,AD∥BC,对角线AC与BD相交于点O,S△AOD=9,S△BOC=16,求S梯形ABCD.
如图,已知梯形ABCD,AD∥BC,对角线AC与BD相交于点O,S△AOD=9,S△BOC=16,求S梯形ABCD. 如图,若数轴上A、B两点所对应的有理数分别为a、b,则|b|-|a|=<0.
如图,若数轴上A、B两点所对应的有理数分别为a、b,则|b|-|a|=<0.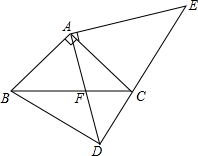 如图,在△ABC和△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C、D、E在同一直线上,连结BD.
如图,在△ABC和△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C、D、E在同一直线上,连结BD.