题目内容
3. 如图,在四边形ABCD中,∠ABC=30°,将△DCB绕点C顺时针旋转60°后,点D的对应点恰好与点A重合,得到△ACE,若AB=3,BC=4,则BD=5(提示:可连接BE)
如图,在四边形ABCD中,∠ABC=30°,将△DCB绕点C顺时针旋转60°后,点D的对应点恰好与点A重合,得到△ACE,若AB=3,BC=4,则BD=5(提示:可连接BE)
分析 要求BD的长,根据旋转的性质,只要求出AE的长即可,由题意可得到三角形ABE的形状,从而可以求得AE的长,本题得以解决.
解答  解:连接BE,如右图所示,
解:连接BE,如右图所示,
∵△DCB绕点C顺时针旋转60°得到△ACE,AB=3,BC=4,∠ABC=30°,
∴∠BCE=60°,CB=CE,AE=BD,
∴△BCE是等边三角形,
∴∠CBE=60°,BE=BC=4,
∴∠ABE=∠ABC+∠CBE=30°+60°=90°,
∴AE=$\sqrt{A{B}^{2}+B{E}^{2}}=\sqrt{{3}^{2}+{4}^{2}}=5$,
又∵AE=BD,
∴BD=5,
故答案为:5.
点评 本题考查旋转的性质,解题的关键是明确题意,找出所求问题需要的条件.

练习册系列答案
相关题目
8.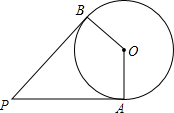 如图,PA、PB是⊙O的切线,切点分别为A、B,若OA=2,∠P=60°,则$\widehat{AB}$的长为( )
如图,PA、PB是⊙O的切线,切点分别为A、B,若OA=2,∠P=60°,则$\widehat{AB}$的长为( )
 如图,PA、PB是⊙O的切线,切点分别为A、B,若OA=2,∠P=60°,则$\widehat{AB}$的长为( )
如图,PA、PB是⊙O的切线,切点分别为A、B,若OA=2,∠P=60°,则$\widehat{AB}$的长为( )| A. | $\frac{2}{3}$π | B. | π | C. | $\frac{4}{3}π$ | D. | $\frac{5}{3}π$ |
15. 如图,直线y=ax+b过点A(0,2)和点B(-3,0),则方程ax+b=0的解是( )
如图,直线y=ax+b过点A(0,2)和点B(-3,0),则方程ax+b=0的解是( )
 如图,直线y=ax+b过点A(0,2)和点B(-3,0),则方程ax+b=0的解是( )
如图,直线y=ax+b过点A(0,2)和点B(-3,0),则方程ax+b=0的解是( )| A. | x=2 | B. | x=0 | C. | x=-1 | D. | x=-3 |
4.下面所给的图形中,是轴对称图形但不是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
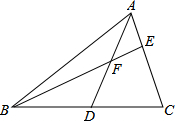 如图,在△ABC中,AD为BC边上的中线,E为AC上的一点,BE交AD于点F,已知AE=EF.求证:AC=BF.
如图,在△ABC中,AD为BC边上的中线,E为AC上的一点,BE交AD于点F,已知AE=EF.求证:AC=BF.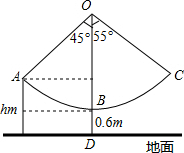 某新农村乐园设置了一个秋千场所,如图所示,秋千拉绳OB的长为3m,静止时,踏板到地面距离BD的长为0.6m(踏板厚度忽略不计).为安全起见,乐园管理处规定:儿童的“安全高度”为hm,成人的“安全高度”为2m(计算结果精确到0.1m)
某新农村乐园设置了一个秋千场所,如图所示,秋千拉绳OB的长为3m,静止时,踏板到地面距离BD的长为0.6m(踏板厚度忽略不计).为安全起见,乐园管理处规定:儿童的“安全高度”为hm,成人的“安全高度”为2m(计算结果精确到0.1m)