题目内容
3.用适当的方法解下列方程(1)(x-1)2=3
(2)x2+2x-2=0
(3)(x-5)2=2(x-5)-1
(4)x(3x-2)=3x-2.
分析 (1)利用直接开平方法解方程;
(2)利用配方法解方程;
(3)先移项得到(x-5)2-2(x-5)+1=0,然后利用因式分解法解方程;
(4)先移项得到x(3x-2)-(3x-2)=0,然后利用因式分解法解方程.
解答 解:(1)x-1=±$\sqrt{3}$,
所以x1=$\sqrt{3}$+1,x2=-$\sqrt{3}$+1;
(2)x2+2x+1=3,
(x+1)2=3,
所以x1=$\sqrt{3}$-1,x2=-$\sqrt{3}$-1;
(4)(x-5)2-2(x-5)+1=0,
[(x-5)-1]2=0,
所以x1=x2=6;
(4)x(3x-2)-(3x-2)=0,
(3x-2)(x-1)=0,
x-1=0或3x-2=0,
所以x1=1,x2=$\frac{2}{3}$.
点评 本题考查了解一元二次方程-因式分解法:先把方程的右边化为0,再把左边通过因式分解化为两个一次因式的积的形式,那么这两个因式的值就都有可能为0,这就能得到两个一元一次方程的解,这样也就把原方程进行了降次,把解一元二次方程转化为解一元一次方程的问题了(数学转化思想).也考查了配方法和直接开平方法解一元二次方程.

练习册系列答案
相关题目
14.已知AB=AC,AD为∠BAC的角平分线,D、E、F…为∠BAC的角平分线上的若干点.如图1,连接BD、CD,图中有1对全等三角形;如图2,连接BD、CD、BE、CE,图中有3对全等三角形;如图3,连接BD、CD、CE、BF、CF,图中有6对全等三角形;依此规律,第8个图形中有全等三角形( )
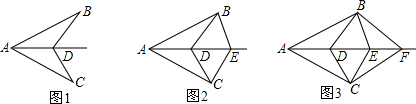

| A. | 24对 | B. | 28对 | C. | 36对 | D. | 72对 |
11.已知式子$\frac{{x}^{2}-4}{2x-4}$的值为零,则x的值为( )
| A. | 2 | B. | -2 | C. | ±2 | D. | 0 |
8.直角三角形的两条直角边的长分别为5,12,则斜边上的高线的长为( )
| A. | $\frac{80}{13}$cm | B. | 13cm | C. | $\frac{13}{2}$cm | D. | $\frac{60}{13}$cm |
15.2x2+4=0的根是( )
| A. | x1=2,x2=-2 | B. | x=2 | C. | 无实根 | D. | 以上均不正确 |
12.等腰三角形的一边为3,另一边为8,则这个三角形的周长为( )
| A. | 14 | B. | 19 | C. | 11 | D. | 14或19 |
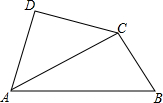 将一副三角尺如图拼接:含30°角的三角尺(△ABC)的长直角边AC与含45°角的三角尺(△ACD)的斜边AC恰好重合.已知AB=2$\sqrt{3}$,P是AC上的一个动点.
将一副三角尺如图拼接:含30°角的三角尺(△ABC)的长直角边AC与含45°角的三角尺(△ACD)的斜边AC恰好重合.已知AB=2$\sqrt{3}$,P是AC上的一个动点.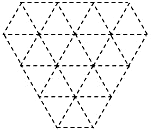 根据题意作出图形,并回答相关问题:请在网格中设计一个图案(图中每个小三角形都是边长为 1的等边三角形),要求所设计的图案既是轴对称图形,又是中心对称图形,并且图案的顶点在格点上,面积等于3$\sqrt{3}$.请将你所设计的图案用铅笔涂黑.
根据题意作出图形,并回答相关问题:请在网格中设计一个图案(图中每个小三角形都是边长为 1的等边三角形),要求所设计的图案既是轴对称图形,又是中心对称图形,并且图案的顶点在格点上,面积等于3$\sqrt{3}$.请将你所设计的图案用铅笔涂黑.