题目内容
13．在方程组$\left\{\begin{array}{l}2x+y=1-m\\ x+2y=2\end{array}\right.$中，若未知数x、y满足x+y＞0，求m的取值范围，并在数轴上表示出来．分析 运用①+②可得x+y的表示式，再运用x+y＞0即可解得m的范围．
解答 解：①+②得3（x+y）=3-m，
∴x+y=-$\frac{1}{3}$m+1，
∵x+y＞0，
∴-$\frac{1}{3}$m+1＞0，
∴m＜3，
用数轴表示为：
点评 本题主要考查了二元一次方程组的解，在数轴上表示不等式的解集及解一元一次不等式，解题的关键是正确的解出x+y的表示式．
练习册系列答案
相关题目
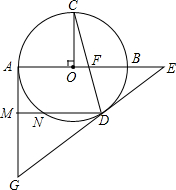如图，AB为⊙O直径，OC⊥AB，弦CD与OB交于点F，过点D、A分别作⊙O的两条切线交于点G，GD交AB延长线于点E，切点为D．
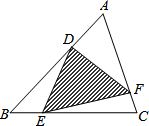如图，△ABC中，点D在AB上，AD=$\frac{1}{3}$AB．点E在BC上，BE=$\frac{1}{4}$BC．点F在AC上，CF=$\frac{1}{5}$CA．已知阴影部分（即△DEF）的面积是25cm2，则△ABC的面积为60 cm2．（写出简要推理）