题目内容
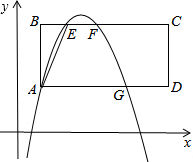 如图所示,已知在平面直角坐标系xOy中,矩形ABCD的一边AD与x轴平行,且边BC,边AD与二次函数y=-x2+bx+c的图象分别交于点E、F和点A、G,其中点A的坐标为(1,2),点E的坐标为(2,m),链结AE,tan∠BAE=
如图所示,已知在平面直角坐标系xOy中,矩形ABCD的一边AD与x轴平行,且边BC,边AD与二次函数y=-x2+bx+c的图象分别交于点E、F和点A、G,其中点A的坐标为(1,2),点E的坐标为(2,m),链结AE,tan∠BAE=| 1 |
| 2 |
(1)求m的值及二次函数的解析式;
(2)求出sin∠EAF的值;
(3)设图象的顶点为M,联结ME、MB,若△MFC与△MEB相似,试求点C的坐标.
考点:二次函数综合题,勾股定理,矩形的性质,相似三角形的判定与性质,锐角三角函数的定义
专题:综合题,分类讨论
分析:(1)在Rt△ABE中运用三角函数可求出m的值,然后运用待定系数法即可解决问题;
(2)过点E作EH⊥AF于点H,如图1.运用勾股定理可求出AE、AF的值,然后在△AEF中运用面积法可求出EH的值,就可解决问题;
(3)过点M作MN⊥EF于N,如图2.易得点M(
,
),求出MN,由对称性可得ME=MF,根据等腰三角形的性质可得EN=NF=
,然后运用勾股定理可求出ME、MF,由ME=MF可得∠MEF=∠MFE,则有∠MEB=∠MFC.据此△MFC与△MEB相似可分两种情况(①若△MFC∽△MEB,②若△MFC∽△BEM)讨论,然后只需运用相似三角形的性质求出FC,就可解决问题.
(2)过点E作EH⊥AF于点H,如图1.运用勾股定理可求出AE、AF的值,然后在△AEF中运用面积法可求出EH的值,就可解决问题;
(3)过点M作MN⊥EF于N,如图2.易得点M(
| 5 |
| 2 |
| 17 |
| 4 |
| 1 |
| 2 |
解答:解:(1)∵四边形ABCD是矩形,∴∠B=90°.
∵A的坐标为(1,2),点E的坐标为(2,m),
∴BE=2-1=1,AB=m-2.
在Rt△ABE中,
∵tan∠BAE=
=
,
∴
=
,
解得:m=4,
∴点E的坐标为(2,4).
∵二次函数y=-x2+bx+c的图象经过点E(2,4)、点A(1,2),
∴
,
解得:
,
∴二次函数的解析式为y=-x2+5x-2;
(2)过点E作EH⊥AF于点H,如图1.
当y=4时,-x2+5x-2=4,
解得:x1=2,x2=3,
∴点F的坐标为(3,4),
∴EF=1.BF=3-1=2,
∴AF=
=
=2
.
∵S△AEF=
EF•AB=
AF•EH,
∴EH=
=
=
.
在Rt△ABE中,
AE=
=
=
,
在Rt△AHE中,
sin∠EAH=
=
=
.
(3)过点M作MN⊥EF于N,如图2.
由y=-x2+5x-2=-(x-
)2+
可得点M(
,
),
∴MN=
-4=
.
由对称性可得ME=MF,
∴EN=NF=
EF=
,
∴ME=MF=
=
=
.
∵ME=MF,
∴∠MEF=∠MFE,
∴∠MEB=∠MFC.
①若△MFC∽△MEB,
则
=
=1,
∴FC=EB=.
∵点F的坐标为(3,4),
∴点C的坐标为(3+1,4)即(4,4);
②若△MFC∽△BEM,
则
=
,
∴FC•BE=MF•EM,
∴FC×1=
×
,
∴FC=
.
∵点F的坐标为(3,4),
∴点C的坐标为(3+
,4)即(
,4).
综上所述:点C的坐标为(4,4)或(
,4).
∵A的坐标为(1,2),点E的坐标为(2,m),
∴BE=2-1=1,AB=m-2.
在Rt△ABE中,
∵tan∠BAE=
| BE |
| AB |
| 1 |
| 2 |
∴
| 1 |
| m-2 |
| 1 |
| 2 |
解得:m=4,
∴点E的坐标为(2,4).
∵二次函数y=-x2+bx+c的图象经过点E(2,4)、点A(1,2),
∴
|
解得:
|
∴二次函数的解析式为y=-x2+5x-2;
(2)过点E作EH⊥AF于点H,如图1.
当y=4时,-x2+5x-2=4,
解得:x1=2,x2=3,
∴点F的坐标为(3,4),
∴EF=1.BF=3-1=2,

∴AF=
| AB2+BF2 |
| 22+22 |
| 2 |
∵S△AEF=
| 1 |
| 2 |
| 1 |
| 2 |
∴EH=
| EF•AB |
| AF |
| 1×2 | ||
2
|
| ||
| 2 |
在Rt△ABE中,
AE=
| AB2+BE2 |
| 22+12 |
| 5 |
在Rt△AHE中,
sin∠EAH=
| EH |
| AE |
| ||||
|
| ||
| 10 |
(3)过点M作MN⊥EF于N,如图2.
由y=-x2+5x-2=-(x-
| 5 |
| 2 |
| 17 |
| 4 |
| 5 |
| 2 |
| 17 |
| 4 |
∴MN=
| 17 |
| 4 |
| 1 |
| 4 |
由对称性可得ME=MF,
∴EN=NF=
| 1 |
| 2 |
| 1 |
| 2 |
∴ME=MF=
| MN2+NF2 |
(
|
| ||
| 4 |

∵ME=MF,
∴∠MEF=∠MFE,
∴∠MEB=∠MFC.
①若△MFC∽△MEB,
则
| FC |
| EB |
| MF |
| ME |
∴FC=EB=.
∵点F的坐标为(3,4),
∴点C的坐标为(3+1,4)即(4,4);
②若△MFC∽△BEM,
则
| FC |
| EM |
| MF |
| BE |
∴FC•BE=MF•EM,
∴FC×1=
| ||
| 4 |
| ||
| 4 |
∴FC=
| 5 |
| 16 |
∵点F的坐标为(3,4),
∴点C的坐标为(3+
| 5 |
| 16 |
| 53 |
| 16 |
综上所述:点C的坐标为(4,4)或(
| 53 |
| 16 |
点评:本题主要考查了运用待定系数法求二次函数的解析式、二次函数的性质、相似三角形的判定与性质、矩形的性质、三角函数的定义、勾股定理等知识,有一定的综合性,构造Rt△AHE是解决第(2)小题的关键,运用相似三角形的性质及分类讨论是解决第(3)小题的关键.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
一次函数y=ax+b交x轴于点(-5,0),则关于x的方程ax+b=0的解是( )
| A、x=5 | B、x=-5 |
| C、x=0 | D、无法求解 |
 如图,在△ABC中,∠B=45°,点D在BC边,DC=3,AD=5,AC=7,求AB的长.
如图,在△ABC中,∠B=45°,点D在BC边,DC=3,AD=5,AC=7,求AB的长. 如图,已知DF⊥AB于点F,且∠A=45°,∠D=30°,求∠ACB的度数.
如图,已知DF⊥AB于点F,且∠A=45°,∠D=30°,求∠ACB的度数. 图中,等边△ABC的边长为acm,D、E分别是AB、AC上的点,将△ADE沿DE折叠,点A落在点A′处,且点A′在△ABC的外部,那么阴影部分图形的周长为( )cm.
图中,等边△ABC的边长为acm,D、E分别是AB、AC上的点,将△ADE沿DE折叠,点A落在点A′处,且点A′在△ABC的外部,那么阴影部分图形的周长为( )cm.