题目内容
已知x=3
+2
，y=3
-2
，则x2-xy+y2= ．
| 2 |
| 3 |
| 2 |
| 3 |
考点：二次根式的化简求值
专题：
分析：把原式化成（x-y）2+xy，然后把x、y的值代入，利用完全平方公式和平方差公式求解．
解答：解：原式=（x-y）2+xy
=（3
+2
-3
+2
）2+（3
+2
）（3
-2
）
=（4
）2+6
=48+6
=54．
故答案是：54．
=（3
| 2 |
| 3 |
| 3 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
=（4
| 3 |
=48+6
=54．
故答案是：54．
点评：本题考查了二次根式的求值，正确把所求的式子进行变形，理解完全平方公式和平方差公式的结构是关键．
练习册系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案
小学暑假作业东南大学出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
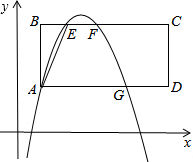如图所示，已知在平面直角坐标系xOy中，矩形ABCD的一边AD与x轴平行，且边BC，边AD与二次函数y=-x2+bx+c的图象分别交于点E、F和点A、G，其中点A的坐标为（1，2），点E的坐标为（2，m），链结AE，tan∠BAE=
如图，点E是∠ABC的平分线与△ABC的外角∠ACD的平分线CE的交点，∠A=64°，你能求出∠E的度数吗？
已知二次函数y=x2+bx-1的图象经过点（3，2）．下列说法，正确的是（ ）
| A、经过一点有且只有一条直线 |
| B、两点确定一条直线 |
| C、两条直线相交至少有两个交点 |
| D、线段AB就是表示点A到点B的距离 |
已知非零向量
，
，
，下列条件中，不能判定
∥
的是（ ）
| a |
| b |
| c |
| a |
| b |
A、|
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|