题目内容
判断下列命题是真命题还是假命题,并说明理由.
(1)两个锐角的和是钝角.
(2)点P到线段AB两端点的距离相等,则点P是线段AB的中点.
(3)不相等的两个角不是对顶角.
(4)若∠1+∠2=90°,∠3+∠2=90°,则∠1=∠3.
(1)两个锐角的和是钝角.
(2)点P到线段AB两端点的距离相等,则点P是线段AB的中点.
(3)不相等的两个角不是对顶角.
(4)若∠1+∠2=90°,∠3+∠2=90°,则∠1=∠3.
考点:命题与定理
专题:
分析:对真命题进行证明,对假命题进行举反例说明,逐题判断即可.
解答:解:(1)假命题,如两个锐角分别为30°和30°,则这两个角的和为60°不是钝角,所以两个锐角的和是钝角不正确;
(2)假命题,由条件可知点P在线段AB的垂直平分线上,所以P点不一定在线段AB上,所以P不是线段AB的中点;
(3)真命题,假如这两个角是对顶角,则这两个角相等,与这两个角不相等矛盾,所以这两个角不是对顶角;
(4)真命题,由∠1+∠2=90°,∠3+∠2=90°,可得∠1=90°-∠2,∠3=90°-∠2,所以∠1=∠3.
(2)假命题,由条件可知点P在线段AB的垂直平分线上,所以P点不一定在线段AB上,所以P不是线段AB的中点;
(3)真命题,假如这两个角是对顶角,则这两个角相等,与这两个角不相等矛盾,所以这两个角不是对顶角;
(4)真命题,由∠1+∠2=90°,∠3+∠2=90°,可得∠1=90°-∠2,∠3=90°-∠2,所以∠1=∠3.
点评:本题主要考查命题的判断,掌握利用举反例判定假命题的方法是解题的关键.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
下列说法,正确的是( )
| A、经过一点有且只有一条直线 |
| B、两点确定一条直线 |
| C、两条直线相交至少有两个交点 |
| D、线段AB就是表示点A到点B的距离 |
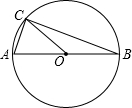 如图,AB是⊙O的直径,点C是圆上一点,∠BAC=70°,则∠OCB=( )
如图,AB是⊙O的直径,点C是圆上一点,∠BAC=70°,则∠OCB=( )| A、35° | B、50° |
| C、20° | D、30° |
已知非零向量
,
,
,下列条件中,不能判定
∥
的是( )
| a |
| b |
| c |
| a |
| b |
A、|
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
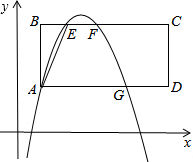 如图所示,已知在平面直角坐标系xOy中,矩形ABCD的一边AD与x轴平行,且边BC,边AD与二次函数y=-x2+bx+c的图象分别交于点E、F和点A、G,其中点A的坐标为(1,2),点E的坐标为(2,m),链结AE,tan∠BAE=
如图所示,已知在平面直角坐标系xOy中,矩形ABCD的一边AD与x轴平行,且边BC,边AD与二次函数y=-x2+bx+c的图象分别交于点E、F和点A、G,其中点A的坐标为(1,2),点E的坐标为(2,m),链结AE,tan∠BAE=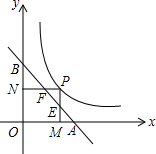 如图,P是函数y=
如图,P是函数y=