题目内容
 如图,在△ABC中,∠B=45°,点D在BC边,DC=3,AD=5,AC=7,求AB的长.
如图,在△ABC中,∠B=45°,点D在BC边,DC=3,AD=5,AC=7,求AB的长.考点:勾股定理
专题:
分析:作AE⊥BC于E,在Rt△AEC与Rt△ADE中根据勾股定理可得出DE的长,求出∠DAE的度数,进而得出AE2的值,再判断出△AEB是等腰直角三角形,根据勾股定理即可得出结论.
解答: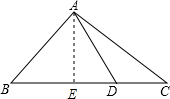 解:作AE⊥BC于E.
解:作AE⊥BC于E.
在Rt△AEC中,AE2=AC2-CE2=AC2-(DC+DE)2=72-(3+DE)2=49-(3+DE)2,
在Rt△ADE中:AE2=AD2-DE2=52-DE2=25-DE2
∴49-(3+DE)2=25-DE2,解得DE=2.5.
∵AD=5=2DE,
∴∠DAE=30°,
∴∠ADE=90°-30°=60°
∴∠ADC=180°-∠ADE=180°-60°=120°,
∴AE2=52-2.52=
.
在Rt△AEB中,
∵∠B=45°
∴△AEB是等腰直角三角形
∴BE=AE
∴AB2=AE2+BE2=2AE2=2×
=
∴AB=
=
.
 解:作AE⊥BC于E.
解:作AE⊥BC于E.在Rt△AEC中,AE2=AC2-CE2=AC2-(DC+DE)2=72-(3+DE)2=49-(3+DE)2,
在Rt△ADE中:AE2=AD2-DE2=52-DE2=25-DE2
∴49-(3+DE)2=25-DE2,解得DE=2.5.
∵AD=5=2DE,
∴∠DAE=30°,
∴∠ADE=90°-30°=60°
∴∠ADC=180°-∠ADE=180°-60°=120°,
∴AE2=52-2.52=
| 75 |
| 4 |
在Rt△AEB中,
∵∠B=45°
∴△AEB是等腰直角三角形
∴BE=AE
∴AB2=AE2+BE2=2AE2=2×
| 75 |
| 4 |
| 75 |
| 2 |
∴AB=
|
5
| ||
| 2 |
点评:本题考查的是勾股定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
 如图所示,AC⊥BC,DE⊥BC,FG⊥AB,∠1=∠2,求证:∠2与∠3互余.
如图所示,AC⊥BC,DE⊥BC,FG⊥AB,∠1=∠2,求证:∠2与∠3互余. 如图,CD∥AB,AB丄AE.求∠ABC+∠BCD.
如图,CD∥AB,AB丄AE.求∠ABC+∠BCD.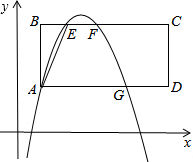 如图所示,已知在平面直角坐标系xOy中,矩形ABCD的一边AD与x轴平行,且边BC,边AD与二次函数y=-x2+bx+c的图象分别交于点E、F和点A、G,其中点A的坐标为(1,2),点E的坐标为(2,m),链结AE,tan∠BAE=
如图所示,已知在平面直角坐标系xOy中,矩形ABCD的一边AD与x轴平行,且边BC,边AD与二次函数y=-x2+bx+c的图象分别交于点E、F和点A、G,其中点A的坐标为(1,2),点E的坐标为(2,m),链结AE,tan∠BAE=