题目内容
如图，已知DF⊥AB于点F，且∠A=45°，∠D=30°，求∠ACB的度数．考点：三角形内角和定理
专题：
分析：由三角形的内角和定理，可得∠AEF=45°，再由对顶角相等得出∠CED=∠AEF=45°，由外角和定理即可求得∠ACB的度数．
解答：解：∵DF⊥AB于点F，
∴∠EFA=90°，
∵∠A=45°，
∴∠AEF=45°，
∴∠CED=∠AEF=45°，
又∵∠D=30°，
∴∠ACB=∠CED+∠D=45°+30°=75°．
∴∠EFA=90°，
∵∠A=45°，
∴∠AEF=45°，
∴∠CED=∠AEF=45°，
又∵∠D=30°，
∴∠ACB=∠CED+∠D=45°+30°=75°．
点评：本题主要考查了三角形的内角和定理，解题的关键是熟记内角和定理及外角和定理．
练习册系列答案
相关题目
如图，CD∥AB，AB丄AE．求∠ABC+∠BCD．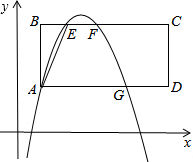
如图所示，已知在平面直角坐标系xOy中，矩形ABCD的一边AD与x轴平行，且边BC，边AD与二次函数y=-x2+bx+c的图象分别交于点E、F和点A、G，其中点A的坐标为（1，2），点E的坐标为（2，m），链结AE，tan∠BAE=
如图所示，将直角边长为6
已知二次函数y=x2+bx-1的图象经过点（3，2）．