题目内容
4. 如图,△ABC中,AB=AC,AD⊥BC垂足为点D,CE⊥AB垂足为点E,AE=CE.
如图,△ABC中,AB=AC,AD⊥BC垂足为点D,CE⊥AB垂足为点E,AE=CE.求证:(1)△AEF≌△CEB;
(2)AF=2CD.
分析 (1)根据等腰三角形三线合一的性质和已知条件易证△AEF≌△CEB;
(2)由(1)可知AF=BC,BC=2CD,所以AF=2CD,问题得证.
解答 解:
(1)证明:∵AD⊥BC,
∴∠B+∠BAD=90°.
∵CE⊥AB,
∴∠B+∠BCE=90°.
∴∠EAF=∠ECB,
在△AEF和△CEB中,
$\left\{{\begin{array}{l}{∠AEF=∠BEC}\\{AE=CE}\\{∠EAF=∠BCE}\end{array}}\right.$,
∴△AEF≌△CEB;
(2)∵△AEF≌△CEB.
∴AF=BC.
∵AB=AC,AD⊥BC.
∴CD=BD,BC=2CD
∴AF=2CD.
点评 本题考查了全等三角形的判定与性质以及等腰三角形三线合一的性质,熟记性质准确确定出全等三角形是解题的关键.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案
相关题目
12.计算tan30°的值等于( )
| A. | $\sqrt{3}$ | B. | 3$\sqrt{3}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\frac{\sqrt{3}}{2}$ |
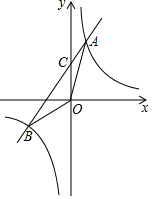 如图,已知反比例函数y=$\frac{8}{x}$与一次函数y=kx+b的图象交于A、B两点,且点A的横坐标是2,点B的纵坐标是-2.求:
如图,已知反比例函数y=$\frac{8}{x}$与一次函数y=kx+b的图象交于A、B两点,且点A的横坐标是2,点B的纵坐标是-2.求: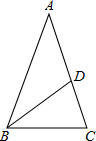 如图,在△ABC中,AB=AC,∠A=36°,BD是∠ABC的角平分线.
如图,在△ABC中,AB=AC,∠A=36°,BD是∠ABC的角平分线.