题目内容
13.计算$\frac{2006}{200{6}^{2}-2005×2007}$.分析 由2005×2007=(2006-1)(2006+1)=20062-1,再去括号、合并可得.
解答 解:原式=$\frac{2006}{200{6}^{2}-(2006-1)(2006+1)}$
=$\frac{2006}{200{6}^{2}-(200{6}^{2}-1)}$
=$\frac{2006}{200{6}^{2}-200{6}^{2}+1}$
=2006.
点评 本题主要考查平方差公式,应用平方差公式计算时,应注意以下几个问题:①左边是两个二项式相乘,并且这两个二项式中有一项完全相同,另一项互为相反数;②右边是相同项的平方减去相反项的平方;③公式中的a和b可以是具体数,也可以是单项式或多项式;④对形如两数和与这两数差相乘的算式,都可以运用这个公式计算,且会比用多项式乘以多项式法则简便.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
4.已知二次函数y=2x2-7x+3,若y随x的增大而增大,则x的取值范围是( )
| A. | x>$\frac{7}{2}$ | B. | x<$\frac{7}{2}$ | C. | x<-$\frac{7}{2}$ | D. | x>-$\frac{7}{2}$ |
1.移动互联网已经全面进入人们的日常生活,截至2016年9月,全国4G用户总数达到1.62亿,其中1.62亿用科学记数法表示为( )
| A. | 1.62×104 | B. | 162×106 | C. | 1.62×108 | D. | 0.162×109 |
18.下列分式是最简分式的是( )
| A. | $\frac{4}{2x}$ | B. | $\frac{x-1}{{{x^2}-1}}$ | C. | $\frac{2x}{{{x^2}+1}}$ | D. | $\frac{1-x}{x-1}$ |
5.一元二次方程x(x-1)=2(x-1)2的解为( )
| A. | 1 | B. | 2 | C. | 1和2 | D. | 1和-2 |
2.把三角形的面积分为相等的两部分的是( )
| A. | 三角形的中线 | B. | 三角形的角平分线 | ||
| C. | 三角形的高 | D. | 以上都不对 |
3.三角形的两边长分别为3米和6米,第三边的长是方程x2-6x+8=0的一个根,则这个三角形的周长为( )
| A. | 11 | B. | 12 | C. | 11或 13 | D. | 13 |
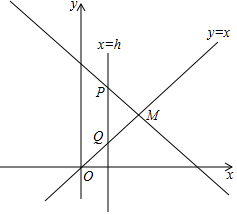 如图,直线y=x和直线y=-x+5相交于点M,直线PQ⊥x轴,分别交直线y=-x+5和直线y=x于点P、Q,点R是y轴上一点,若△PQR为等腰直角三角形.求点R的坐标.
如图,直线y=x和直线y=-x+5相交于点M,直线PQ⊥x轴,分别交直线y=-x+5和直线y=x于点P、Q,点R是y轴上一点,若△PQR为等腰直角三角形.求点R的坐标.