题目内容
3．三角形的两边长分别为3米和6米，第三边的长是方程x2-6x+8=0的一个根，则这个三角形的周长为（ ）| A． | 11 | B． | 12 | C． | 11或 13 | D． | 13 |
分析 解方程求得x的值，再根据三角形三边之间的关系得出符合条件的x的值，最后求出周长即可．
解答 解：∵x2-6x+8=0，即（x-2）（x-4）=0，
∴x-2=0或x-4=0，
解得：x=2或x=4，
若x=2，则三角形的三边2+3＜6，构不成三角形，舍去；
当x=4时，这个三角形的周长为3+4+6=13，
故选：D．
点评 本题考查了一元二次方程的解法及三角形三边之间的关系．解一元二次方程常用的方法有直接开平方法，配方法，公式法，因式分解法，要根据方程的特点灵活选用合适的方法．
练习册系列答案
阅读快车系列答案
相关题目
14．用反证法证明命题“三角形中必有一个内角小于或等于60°”时，首先应假设这个三角形中（ ）
| A． | 每一个内角都大于60° | B． | 每一个内角都小于60° | ||
| C． | 有一个内角大于60° | D． | 有一个内角小于60° |
11．方程（x-5）（x+3）=x+3的解是（ ）
| A． | x=5 | B． | x=-3 | C． | x=5或x=-3 | D． | x=-3或x=6 |
18．方程x2+2x+3=0的两根的情况是（ ）
| A． | 有两个不相等的实数根 | B． | 没有实数根 | ||
| C． | 有两个相同的实数根 | D． | 不能确定 |
8．在直角坐标系中，点P的坐标为（-3，2），则和点P关于原点中心对称的点P′的坐标是 （ ）
| A． | （-3，2） | B． | （-3，-2） | C． | （3，2） | D． | （3，-2） |
15．下列命题是假命题的是（ ）
| A． | 所有的实数都可用数轴上的点表示 | B． | 同位角相等，两直线平行 | ||
| C． | 无理数包括正无理数，0，负无理数 | D． | 两点之间，线段最短 |
12．下列方程是一元二次方程的是（ ）
| A． | ax2+bx+c=0 | B． | x2-4x+3=0 | C． | x2+2x=x2-1 | D． | $\frac{1}{{x}^{2}}$-x=2 |
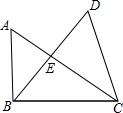图中有几个三角形？用符号表示这些三角形．