题目内容
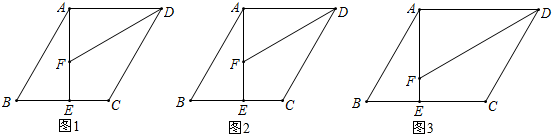
 如图,开发区为提高某段海堤的防潮能力,将长1000m的一堤段(原海堤的横断面如图中的梯形ABCD)的堤面加宽1.6m,将原来的背水坡度AD(坡比1:1)改成现在的背水坡(坡比1:2),已知AD=8.0m,求完成这一工程所需的土方.
如图,开发区为提高某段海堤的防潮能力,将长1000m的一堤段(原海堤的横断面如图中的梯形ABCD)的堤面加宽1.6m,将原来的背水坡度AD(坡比1:1)改成现在的背水坡(坡比1:2),已知AD=8.0m,求完成这一工程所需的土方.考点:解直角三角形的应用-坡度坡角问题
专题:
分析:过点D、E向下底引垂线,得到两个直角三角形,利用三角函数分别求得增加的下底宽和高的相应线段.所需的土方=增加横截面的面积×长度1000.
解答: 解:分别作DM⊥AB交AB于M,EN⊥AB交AB于N.
解:分别作DM⊥AB交AB于M,EN⊥AB交AB于N.
∵
=
,
∴∠DAM=45°,△ADM为等腰三角形,
∵AD=8m,
∴DM=AM=4
m.
又∵CD∥AB,
∴EN=DM=4
m,
DE=MN=1.6m.
在Rt△FNE中,
=
,
∴FN=2EN=8
m.
∴FA=FN+NM-AM=8
+1.6-4
=(4
+1.6)m.
S四边形ADEF=
(AF+DE)•EN=
(4
+1.6+1.6)×4
=(
+16)m2,
V体积=S四边形ADEF×1000=(
+16)×1000=(6400
+16000)m3.
答:完成这一工程需6400
+16000m3的土方.
 解:分别作DM⊥AB交AB于M,EN⊥AB交AB于N.
解:分别作DM⊥AB交AB于M,EN⊥AB交AB于N.∵
| DM |
| AM |
| 1 |
| 1 |
∴∠DAM=45°,△ADM为等腰三角形,
∵AD=8m,
∴DM=AM=4
| 2 |
又∵CD∥AB,
∴EN=DM=4
| 2 |
DE=MN=1.6m.
在Rt△FNE中,
| EN |
| FN |
| 1 |
| 2 |
∴FN=2EN=8
| 2 |
∴FA=FN+NM-AM=8
| 2 |
| 2 |
| 2 |
S四边形ADEF=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
32
| ||
| 5 |
V体积=S四边形ADEF×1000=(
32
| ||
| 5 |
| 2 |
答:完成这一工程需6400
| 2 |
点评:本题考查了锐角三角函数的应用.需注意构造直角三角形是常用的辅助线方法.

练习册系列答案
相关题目
 用反证法证明:如图所示,已知a⊥c,b⊥c,那么a∥b.
用反证法证明:如图所示,已知a⊥c,b⊥c,那么a∥b. 如图,直线AB、MN、PQ相交于点O,∠BOM是它的余角的2倍,∠AOP=2∠MOQ,且有OG⊥OA,求∠POG的度数.
如图,直线AB、MN、PQ相交于点O,∠BOM是它的余角的2倍,∠AOP=2∠MOQ,且有OG⊥OA,求∠POG的度数.