题目内容
已知:在平行四边形ABCD中,AE⊥BC于E,DF平分∠ADC交线段AE于F.
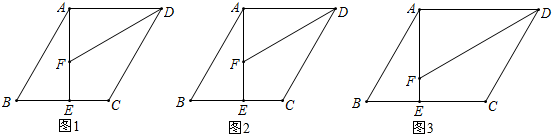
(1)如图1,若AE=AD,∠ADC=60°,请直接写出CD、AF、BE三条线段之间的数量关系;
(2)如图2,若AE=AD,你在(1)中得到的结论是否依然成立?若成立,请证明;若不成立,请说明理由;
(3)如图3,若
=
,试探究CD、AF、BE三条线段之间的数量关系,并证明.
(1)如图1,若AE=AD,∠ADC=60°,请直接写出CD、AF、BE三条线段之间的数量关系;
(2)如图2,若AE=AD,你在(1)中得到的结论是否依然成立?若成立,请证明;若不成立,请说明理由;
(3)如图3,若
| AE |
| AD |
| m |
| n |

考点:相似三角形的判定与性质,全等三角形的判定与性质,平行四边形的性质
专题:
分析:(1)求出BE=
AB,证△ADF≌△EAB,推出AF=BE,即可得出答案.
(2)延长FA至G,使AG=BE,证△GAD≌△BEA,推出DG=AB,求出GD=GF,即可推出答案;
(3)延长EA至G,使
=
,连结DG,证△GAD∽△BEA,推出DG=
AB=
CD,同理可得GD=GF=AG+AF=
BE+AF,即可推出答案.
| 1 |
| 2 |
(2)延长FA至G,使AG=BE,证△GAD≌△BEA,推出DG=AB,求出GD=GF,即可推出答案;
(3)延长EA至G,使
| BE |
| AG |
| m |
| n |
| n |
| m |
| n |
| m |
| n |
| m |
解答: 解:(1)CD=AF+BE,
解:(1)CD=AF+BE,
理由是:如图1,∵∠ADC=60°,DF平分∠ADC,
∴∠ADF=∠CDF=30°,
∵平行四边形ABCD,
∴∠B=∠ADC=60°,AD∥BC,AB=CD,
∵AE⊥BC,
∴∠DAF=∠AEB=90°,
∴∠BAE=30°=∠ADF,
∴BE=
AB=
CD,
在△ADF和△EAB中,
,
∴△ADF≌△EAB(ASA),
∴AF=BE=
CD,
∴CD=AF+BE.
(2)结论仍然成立.
证明:如图2,延长FA至G,使AG=BE,
在△DAG和△AEB中,
,
∴△DAG≌△AEB(SAS),
∴∠GDA=∠BAE,GD=AB=CD,
又∵平行四边形ABCD中,AE⊥BC,
∴∠BAE+∠ADC=90°,
∴∠GDF=90°-∠CDF,
在Rt△DAF中,∠AFD=90°-∠ADF,
∴∠GFD=∠GDF,
∴GF=GD,
∴GD=AF+AG,
∴CD=AF+BE.
(3)CD=BE+
AF,
如图2,延长EA至G,使
=
,连结DG,
则
=
=
,∠AEB=∠DAG,
∴△ABE∽△DGA,
∴
=
,
∴DG=
AB=
CD;
同理(2)可得GD=GF=AG+AF=
BE+AF,
∴
CD=
BE+AF;
∴CD=BE+
AF.
 解:(1)CD=AF+BE,
解:(1)CD=AF+BE,理由是:如图1,∵∠ADC=60°,DF平分∠ADC,
∴∠ADF=∠CDF=30°,
∵平行四边形ABCD,
∴∠B=∠ADC=60°,AD∥BC,AB=CD,
∵AE⊥BC,
∴∠DAF=∠AEB=90°,
∴∠BAE=30°=∠ADF,
∴BE=
| 1 |
| 2 |
| 1 |
| 2 |
在△ADF和△EAB中,
|
∴△ADF≌△EAB(ASA),
∴AF=BE=
| 1 |
| 2 |
∴CD=AF+BE.
(2)结论仍然成立.
证明:如图2,延长FA至G,使AG=BE,
在△DAG和△AEB中,
|
∴△DAG≌△AEB(SAS),
∴∠GDA=∠BAE,GD=AB=CD,
又∵平行四边形ABCD中,AE⊥BC,
∴∠BAE+∠ADC=90°,
∴∠GDF=90°-∠CDF,
在Rt△DAF中,∠AFD=90°-∠ADF,
∴∠GFD=∠GDF,
∴GF=GD,
∴GD=AF+AG,
∴CD=AF+BE.
(3)CD=BE+
| m |
| n |
如图2,延长EA至G,使
| BE |
| AG |
| m |
| n |
则
| BE |
| AG |
| AE |
| AD |
| m |
| n |
∴△ABE∽△DGA,
∴
| AB |
| DG |
| m |
| n |
∴DG=
| n |
| m |
| n |
| m |
同理(2)可得GD=GF=AG+AF=
| n |
| m |
∴
| n |
| m |
| n |
| m |
∴CD=BE+
| m |
| n |
点评:本题考查了相似三角形的判定和性质以及全等三角形的性质和判定,平行四边形的性质的应用,主要考查学生运用定理进行推理的能力.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
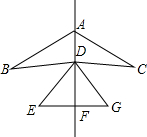 如图是一个风筝的图案,它是以直线为对称轴的轴对称图形,下列结论中不一定成立的是( )
如图是一个风筝的图案,它是以直线为对称轴的轴对称图形,下列结论中不一定成立的是( )| A、△ABD≌△ACD |
| B、AF垂直平分EG |
| C、直线BG,CE的交点在AF上 |
| D、△DEG是等边三角形 |
 如图,开发区为提高某段海堤的防潮能力,将长1000m的一堤段(原海堤的横断面如图中的梯形ABCD)的堤面加宽1.6m,将原来的背水坡度AD(坡比1:1)改成现在的背水坡(坡比1:2),已知AD=8.0m,求完成这一工程所需的土方.
如图,开发区为提高某段海堤的防潮能力,将长1000m的一堤段(原海堤的横断面如图中的梯形ABCD)的堤面加宽1.6m,将原来的背水坡度AD(坡比1:1)改成现在的背水坡(坡比1:2),已知AD=8.0m,求完成这一工程所需的土方.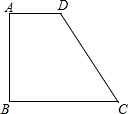 如图,直角梯形ABCD中,∠B=90°,AD∥BC,并且AD+BC=CD,求证:以AB为直径的⊙O与斜腰CD相切.
如图,直角梯形ABCD中,∠B=90°,AD∥BC,并且AD+BC=CD,求证:以AB为直径的⊙O与斜腰CD相切.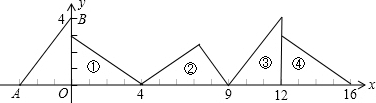
 如图,AC平分∠BCD,AB=AD,AE⊥BC于点E,AF⊥CD于点F.
如图,AC平分∠BCD,AB=AD,AE⊥BC于点E,AF⊥CD于点F. 如图,直线AB、CD相交于点O,OE是∠COB的平分线,∠EOF=90°,∠AOD=70°,则∠COF的度数为
如图,直线AB、CD相交于点O,OE是∠COB的平分线,∠EOF=90°,∠AOD=70°,则∠COF的度数为