题目内容
14.已知(x+y)2=8,(x-y)2=2,则x2+y2+xy=$\frac{13}{2}$.分析 先根据题意得出x2+y2的值,再求出xy的值,代入代数式进行计算即可.
解答 解:∵(x+y)2=8,(x-y)2=2,
∴x2+y2+2xy=8①,x2+y2-2xy=2②,
∴①+②得,x2+y2=5,①-②得,xy=$\frac{3}{2}$,
∴x2+y2+xy=5+$\frac{3}{2}$=$\frac{13}{2}$.
故答案为:$\frac{13}{2}$.
点评 本题考查的是完全平方公式,熟记公式是解答此题的关键.

练习册系列答案
相关题目
2.化简下列各式
(1)3a(a+1)-(3+a)(3-a)-(2a-1)2
(2)($\frac{{x}^{2}-2x+4}{x-1}$+2-x)÷$\frac{{x}^{2}+4x+4}{1-x}$.
(1)3a(a+1)-(3+a)(3-a)-(2a-1)2
(2)($\frac{{x}^{2}-2x+4}{x-1}$+2-x)÷$\frac{{x}^{2}+4x+4}{1-x}$.
9.△ABC中,AB=2,AC=x,中线AD=4,则x的值可能是( )
| A. | 12 | B. | 14 | C. | 16 | D. | 8 |
19.下列式子是分式的是( )
| A. | $\frac{x}{2}$ | B. | $\frac{3}{x+1}$ | C. | $\frac{x}{2}+y$ | D. | $\frac{x}{π}$ |
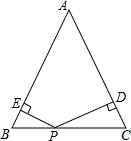 如图,△ABC中,AB=AC=4,P是BC上任意一点,过P作PD⊥AC于D,PE⊥AB于E,若S△ABC=6,则PE+PD=3.
如图,△ABC中,AB=AC=4,P是BC上任意一点,过P作PD⊥AC于D,PE⊥AB于E,若S△ABC=6,则PE+PD=3.