题目内容
7. 如图,直线l上有三个正方形a,b,c,若a,c的面积分别为7和9,则b的面积为( )
如图,直线l上有三个正方形a,b,c,若a,c的面积分别为7和9,则b的面积为( )| A. | 16 | B. | 2 | C. | 32 | D. | 130 |
分析 运用正方形边长相等,再根据同角的余角相等可得∠BAC=∠DCE,然后证明△ACB≌△DCE,再结合全等三角形的性质和勾股定理来求解即可.
解答 解:由于a、b、c都是正方形,所以AC=CD,∠ACD=90°;
∵∠ACB+∠DCE=∠ACB+∠BAC=90°,即∠BAC=∠DCE,
在△ABC和△CED中,
$\left\{\begin{array}{l}{∠ACB=∠CDE}\\{∠ABC=∠DEC=90°}\\{AC=DC}\end{array}\right.$,
∴△ACB≌△DCE(AAS),
∴AB=CE,BC=DE;
在Rt△ABC中,由勾股定理得:AC2=AB2+BC2=AB2+DE2=7+9=16,
即Sb=16,
则b的面积为16,
故选A.
点评 此题主要考查对全等三角形和勾股定理的综合运用,关键是证明△ACB≌△DCE.

练习册系列答案
相关题目
17.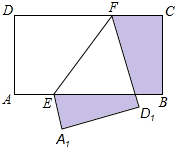 如图,在长方形ABCD中,AB=13,BC=7,点E,F分别在AB,CD上,将长方形ABCD沿EF折叠.使点A,D分别落在长方形ABCD外部的点A1,D1处,则阴影部分图形的周长为( )
如图,在长方形ABCD中,AB=13,BC=7,点E,F分别在AB,CD上,将长方形ABCD沿EF折叠.使点A,D分别落在长方形ABCD外部的点A1,D1处,则阴影部分图形的周长为( )
 如图,在长方形ABCD中,AB=13,BC=7,点E,F分别在AB,CD上,将长方形ABCD沿EF折叠.使点A,D分别落在长方形ABCD外部的点A1,D1处,则阴影部分图形的周长为( )
如图,在长方形ABCD中,AB=13,BC=7,点E,F分别在AB,CD上,将长方形ABCD沿EF折叠.使点A,D分别落在长方形ABCD外部的点A1,D1处,则阴影部分图形的周长为( )| A. | 20 | B. | 40 | C. | 36 | D. | 30 |
19.将二次函数y=x2的图象向下平移2个单位,再向右平移3个单位,则平移后的二次函数的解析式为( )
| A. | y=x2-2 | B. | y=x2+2 | C. | y=(x+3)2+2 | D. | y=(x-3)2-2 |
16.已知二次函数y=-x2+bx+c中,函数y与自变量x之间的部分对应值如表所示,点A(x1,y1),B(x2,y2)在函数的图象上,当0<x1<1,2<x2<3时,y1与y2的大小关系正确的是( )
| x | … | 0 | 1 | 2 | 3 | … |
| y | … | -1 | 2 | 3 | 2 | … |
| A. | y1>y2 | B. | y1≤y2 | C. | y1<y2 | D. | y1≥y2 |
17.若关于x的不等式3-x>a的解集为x<4,则关于m的不等式2m+3a<1的解为( )
| A. | m<2 | B. | m>1 | C. | m>-2 | D. | m<-1 |