题目内容
6.已知x+2y=$\frac{y-x}{4}$=$\frac{2x+1}{3}$=z,则x,y,z的值为( )| A. | $\left\{\begin{array}{l}{x=\frac{5}{23}}\\{y=-\frac{7}{23}}\\{z=\frac{27}{23}}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=\frac{7}{23}}\\{y=-\frac{5}{23}}\\{z=\frac{3}{23}}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{x=-\frac{7}{23}}\\{y=\frac{5}{23}}\\{z=\frac{3}{23}}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=-\frac{5}{23}}\\{y=-\frac{7}{23}}\\{z=\frac{3}{23}}\end{array}\right.$ |
分析 先转化成三元一次方程组,整理后①-②×5得出-23y=-5,求出y值,把y的代入②得出x+$\frac{30}{23}$=1,求出x值,最后把x、y的值代入③求出z即可.
解答 解:∵x+2y=$\frac{y-x}{4}$=$\frac{2x+1}{3}$=z,
∴$\left\{\begin{array}{l}{x+2y=\frac{y-x}{4}}\\{x+2y=\frac{2x+1}{3}}\\{x+2y=z}\end{array}\right.$
整理得:$\left\{\begin{array}{l}{5x+7y=0①}\\{x+6y=1②}\\{x+2y=z③}\end{array}\right.$
①-②×5得:-23y=-5,
解得:y=$\frac{5}{23}$,
把y=$\frac{5}{23}$代入②得:x+$\frac{30}{23}$=1,
解得:x=-$\frac{7}{23}$,
把x、y的值代入③得:z=-$\frac{7}{23}$+$\frac{10}{23}$=$\frac{3}{23}$,
所以原方程组的解为:$\left\{\begin{array}{l}{x=-\frac{7}{23}}\\{y=\frac{5}{23}}\\{z=\frac{3}{23}}\end{array}\right.$,
故选C.
点评 本题考查了解三元一次方程组的应用,解此题的关键是能把三元一次方程组转化成二元一次方程组,难度适中.

练习册系列答案
相关题目

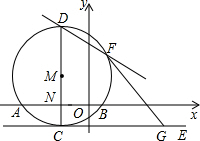 如图,⊙M与x轴交于A、B两点,其坐标分别为A(-3,0)、B(1,0),直径CD⊥x轴于N,抛物线y=-x2-2x+m经过A、B、D三点,
如图,⊙M与x轴交于A、B两点,其坐标分别为A(-3,0)、B(1,0),直径CD⊥x轴于N,抛物线y=-x2-2x+m经过A、B、D三点,
 如图,梯形ABCD中,∠A=120°,BD平分∠ABC,且∠ABC=60°,求∠ADB的度数.
如图,梯形ABCD中,∠A=120°,BD平分∠ABC,且∠ABC=60°,求∠ADB的度数. 如图,在平行四边形ABCD中,E,F分别是AB,CD的中点,若AD⊥BD,问四边形BEDF是什么特殊的四边形?
如图,在平行四边形ABCD中,E,F分别是AB,CD的中点,若AD⊥BD,问四边形BEDF是什么特殊的四边形?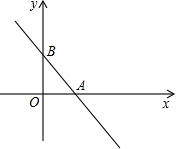 已知:一次函数y=-$\frac{4}{3}$x+4的函数与x轴、y轴交于A、B两点.
已知:一次函数y=-$\frac{4}{3}$x+4的函数与x轴、y轴交于A、B两点.