题目内容
15. 如图,在平行四边形ABCD中,E,F分别是AB,CD的中点,若AD⊥BD,问四边形BEDF是什么特殊的四边形?
如图,在平行四边形ABCD中,E,F分别是AB,CD的中点,若AD⊥BD,问四边形BEDF是什么特殊的四边形?
分析 根据直角三角形斜边上中线求出DE=BE,根据平行四边形性质得出DC=AB,DC∥AB,推出BE=DF,得出平行四边形BFDE,根据菱形的判定推出即可.
解答 解:四边形BEDF是菱形,
∵AD⊥BD,
∴△ABD是直角三角形,且AB是斜边,
∵E为AB的中点,
∴DE=$\frac{1}{2}$AB=BE,
∵四边形ABCD是平行四边形,
∴DC∥AB,DC=AB,
∵F为DC中点,E为AB中点,
∴DF=$\frac{1}{2}$DC,BE=$\frac{1}{2}$AB,
∴DF=BE,DF∥BE,
∴四边形DFBE是平行四边形,
∵DE=EB,
∴四边形BFDE是菱形.
点评 本题考查了平行四边形的性质和判定,菱形的判定,直角三角形斜边上中线等知识点的应用,关键是证出DE=BE和推出平行四边形BEDF.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
6.已知x+2y=$\frac{y-x}{4}$=$\frac{2x+1}{3}$=z,则x,y,z的值为( )
| A. | $\left\{\begin{array}{l}{x=\frac{5}{23}}\\{y=-\frac{7}{23}}\\{z=\frac{27}{23}}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=\frac{7}{23}}\\{y=-\frac{5}{23}}\\{z=\frac{3}{23}}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{x=-\frac{7}{23}}\\{y=\frac{5}{23}}\\{z=\frac{3}{23}}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=-\frac{5}{23}}\\{y=-\frac{7}{23}}\\{z=\frac{3}{23}}\end{array}\right.$ |
5.已知MN是⊙O的一条非直径的弦,则下列说法中错误的是( )
| A. | M、N两点到圆心O的距离相等 | |
| B. | MN是圆的一条对称轴 | |
| C. | 在圆中可画无数条与MN相等的弦 | |
| D. | 圆上有两条弧,一条是优弧,一条是劣弧 |
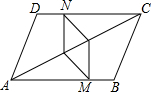 如图,在?ABCD中,CN=AM,AE=CF,求证:四边形MENF是平行四边形.
如图,在?ABCD中,CN=AM,AE=CF,求证:四边形MENF是平行四边形.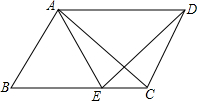 如图所示,在平行四边形ABCD中,E为BC边上一点,且AB=AE,求证:△ABC≌△EAD.
如图所示,在平行四边形ABCD中,E为BC边上一点,且AB=AE,求证:△ABC≌△EAD.