题目内容
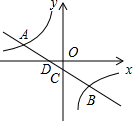 如图,一次函数y=kx+b的图象与反比例函数y=
如图,一次函数y=kx+b的图象与反比例函数y=| m |
| x |
(1)求上述反比例函数和一次函数的解析式;
(2)直接写出当kx+b>
| m |
| x |
考点:反比例函数与一次函数的交点问题
专题:
分析:(1)由一次函数与反比例函数图象交于A和B点,将A的坐标代入反比例函数解析式中,求出m的值,确定出反比例函数解析式,将M坐标代入反比例函数解析式中,即可求出n的值,确定出B的坐标,将A和B坐标代入一次函数解析式中,得到关于k与b的方程组,求出方程组的解得到k与b的值,即可确定出一次函数解析式.
(2)根据A、B的横坐标,结合图象即可得出答案.
(2)根据A、B的横坐标,结合图象即可得出答案.
解答:解:(1)一次函数y=kx+b的图象与反比例函数y=
的图象交于A(-3,1)、B(2,n)两点,
将x=-3,y=1代入反比例函数解析式得:1=
,解得:m=-3,
∴反比例函数解析式为y=-
,
将x=2,y=n代入反比例解析式得:n=
=-
,
∴B(2,-
),又A(-3,1),
将A和B坐标代入一次函数解析式得:
,
解得:
.
故一次函数解析式为y=-
x-
.
(2)根据图象和A、B的坐标得出当kx+b>
时x的取值范围是x<-3或0<x<2.
| m |
| x |
将x=-3,y=1代入反比例函数解析式得:1=
| m |
| -3 |
∴反比例函数解析式为y=-
| 3 |
| x |
将x=2,y=n代入反比例解析式得:n=
| -3 |
| 2 |
| 3 |
| 2 |
∴B(2,-
| 3 |
| 2 |
将A和B坐标代入一次函数解析式得:
|
解得:
|
故一次函数解析式为y=-
| 1 |
| 2 |
| 1 |
| 2 |
(2)根据图象和A、B的坐标得出当kx+b>
| m |
| x |
点评:本题考查了一次函数与反比例函数的交点问题,用待定系数法求一次函数的解析式等知识点,主要考查学生的计算能力和观察图形的能力,用了数形结合思想.

练习册系列答案
相关题目
已知实数(x2-x)2-4(x2-x)-12=0,则代数式x2-x+1的值为( )
| A、-1 | B、7 |
| C、-1或7 | D、以上全不正确 |
 如图所示,MN为⊙O的弦,∠N=52°,则∠MON的度数为( )??
如图所示,MN为⊙O的弦,∠N=52°,则∠MON的度数为( )??| A、38° | B、52°? |
| C、76° | D、104° |


 如图,直线y=kx-2与双曲线y=
如图,直线y=kx-2与双曲线y=