题目内容
14.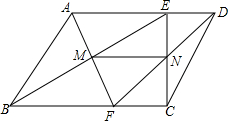 如图,在平行四边形ABCD中,E,F分别是AD,BC上的点,且AE=BF,BE交AF于M,CE交DF于N,求证:MN$\stackrel{∥}{=}$$\frac{1}{2}$AD.
如图,在平行四边形ABCD中,E,F分别是AD,BC上的点,且AE=BF,BE交AF于M,CE交DF于N,求证:MN$\stackrel{∥}{=}$$\frac{1}{2}$AD.
分析 证明△AEM≌△FMB即可证明AM=MF,同理DN=NF,即MN是△ADF的中位线,根据三角形中位线定理证得.
解答 证明:∵平行四边形ABCD中,AD∥BC.
∴∠DAF=∠AFB,
∴在△AEM和△FMB中,$\left\{\begin{array}{l}{∠DAM=∠AFB}\\{∠AME=∠FMB}\\{AE=BF}\end{array}\right.$,
∴△AEM≌△FMB,
∴AM=MF,
同理,DN=NF,
∴MN是△ADF的中位线,
∴MN$\stackrel{∥}{=}$$\frac{1}{2}$AD.
点评 本题考查了三角形的中位线定理,三角形的中位线平行于第三边且等于第三边的一半.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
6.某水果店总共筹备了5.1万资金计划购入一些时令水果销售(品种及价格如下表所示).现租用一辆载货量2.4吨的小货车进货(租金600元),要求将余下资金全部用于采购水果并使得所购水果装满货车.问应该怎样安排进货才能使水果店在销售完这批水果后获利最多?此时最大销售利润为多少元?
| 水果名称 | 进货价(元/千克) | 销售价(元/千克) |
| 凤梨 | 10 | 19 |
| 芒果 | 26 | 36 |
| 荔枝 | 22 | 30 |
3.下列各实数中,最小的是( )
| A. | -π | B. | (-1)0 | C. | $\root{3}{-1}$ | D. | |-2| |
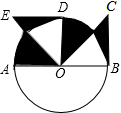 如图,AB是⊙O的直径,过点B作BC⊥OB,且BC=OB,点C在AB的上方,连接OC,△OBC绕着点O逆时针旋转90°得到△ODE
如图,AB是⊙O的直径,过点B作BC⊥OB,且BC=OB,点C在AB的上方,连接OC,△OBC绕着点O逆时针旋转90°得到△ODE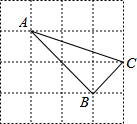 如图,由边长为1的小正方形组成的网格中,A、B、C三点都在网格的格点上.则tan∠BAC=$\frac{1}{2}$.
如图,由边长为1的小正方形组成的网格中,A、B、C三点都在网格的格点上.则tan∠BAC=$\frac{1}{2}$.