题目内容
15.以方程组$\left\{\begin{array}{l}y-x=1\\ y+x=2\end{array}\right.$的解为坐标的点(x,y)在第( )| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
分析 先解方程组得到x和y的值,然后依据各象限内点的坐标特点求解即可.
解答 解:解方程组$\left\{\begin{array}{l}y-x=1\\ y+x=2\end{array}\right.$,得$\left\{\begin{array}{l}{x=\frac{1}{2}}\\{y=\frac{3}{2}}\end{array}\right.$,
所以点($\frac{1}{2}$,$\frac{3}{2}$)在第一象限.
故选A.
点评 本题考查了二元一次方程组的解的定义:一般地,二元一次方程组的两个方程的公共解,叫做二元一次方程组的解.也考查了各象限内点的坐标特点.正确求出方程组的解是解题的关键.

练习册系列答案
相关题目
5.下列各式,计算正确的是( )
| A. | $\sqrt{2}+\sqrt{3}=\sqrt{5}$ | B. | 3$\sqrt{2}-\sqrt{2}$=3 | C. | 2$\sqrt{3}×3\sqrt{3}=6\sqrt{3}$ | D. | ($\sqrt{8}-\sqrt{6}$)$÷\sqrt{2}=2-\sqrt{3}$ |
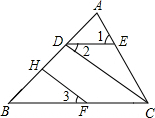
7. 如图,在△ABC中,AB=AC,且AE=AD,∠EDC=α,则∠BAD=( )
如图,在△ABC中,AB=AC,且AE=AD,∠EDC=α,则∠BAD=( )
 如图,在△ABC中,AB=AC,且AE=AD,∠EDC=α,则∠BAD=( )
如图,在△ABC中,AB=AC,且AE=AD,∠EDC=α,则∠BAD=( )| A. | α | B. | 2α | C. | 3α | D. | 4α |
 填空并完成以下证明:
填空并完成以下证明: 如图,已知△ABC为等腰三角形,AB=AC,延长CB和BC至点D、点E,使得BD=CE,试说明AD=AE.
如图,已知△ABC为等腰三角形,AB=AC,延长CB和BC至点D、点E,使得BD=CE,试说明AD=AE.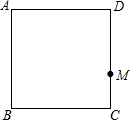 如图,在正方形ABCD中,点M在CD边上,点N在正方形ABCD外部,且满足∠CMN=90°,CM=MN.连接AN,CN,取AN的中点E,连接BE,AC,交于F点.
如图,在正方形ABCD中,点M在CD边上,点N在正方形ABCD外部,且满足∠CMN=90°,CM=MN.连接AN,CN,取AN的中点E,连接BE,AC,交于F点. 如图,将长方形ABCD沿折痕EF对折,使点C与点A重合,若∠AEB=50°,则∠AFE=65°.
如图,将长方形ABCD沿折痕EF对折,使点C与点A重合,若∠AEB=50°,则∠AFE=65°.