题目内容
4. 如图,将长方形ABCD沿折痕EF对折,使点C与点A重合,若∠AEB=50°,则∠AFE=65°.
如图,将长方形ABCD沿折痕EF对折,使点C与点A重合,若∠AEB=50°,则∠AFE=65°.
分析 由平行线的性质可知∠AFE=∠CEF,结合折叠的特性及角的运算即可得出∠CEF=65°,由此即可得出结论.
解答 解:∵四边形ABCD为长方形,
∴AD∥BC,
∴∠AFE=∠CEF.
由翻折的特性可知:∠AEF=∠CEF,
∵∠AEB+∠AEF+∠CEF=180°,∠AEB=50°,
∴∠CEF=65°.
∴∠AFE=65°.
故答案为:65°.
点评 本题考查了长方形的性质、平行线的性质以及角的计算,解题的关键是求出∠CEF的度数.本题属于基础题,难度不大,解决该题型题目时,根据平行线的性质找出相等或互补的角是关键.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
15.以方程组$\left\{\begin{array}{l}y-x=1\\ y+x=2\end{array}\right.$的解为坐标的点(x,y)在第( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
19.为了比较市场上甲、乙两种电子钟每日走时误差的情况,从这两种电子钟中,各随机抽取10台进行测试,两种电子钟走时误差的数据如表(单位:秒):
(1)计算甲、乙两种电子钟走时误差的平均数;
(2)计算甲、乙两种电子钟走时误差的方差;
(3)根据经验,走时稳定性较好的电子钟质量更优.若两种类型的电子钟价格相同,请问:你买哪种电子钟?为什么?
 | 一 | 二 | 三 | 四 | 五 | 六 | 七 | 八 | 九 | 十 |
| 甲种电子钟 | 1 | -3 | -4 | 4 | 2 | -2 | 2 | -1 | -1 | 2 |
| 乙种电子钟 | 4 | -3 | -1 | 2 | -2 | 1 | -2 | 2 | -2 | 1 |
(2)计算甲、乙两种电子钟走时误差的方差;
(3)根据经验,走时稳定性较好的电子钟质量更优.若两种类型的电子钟价格相同,请问:你买哪种电子钟?为什么?
15.在Rt△ABC中,∠C=90°,a=12,b=5,则c的长为( )
| A. | 13 | B. | 14 | C. | 15 | D. | 16 |
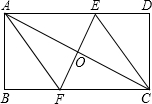 如图,在矩形ABCD中,AB=4cm,BC=8cm,AC的垂直平分线EF分别交AD,BC于点E,F,垂足为点O.
如图,在矩形ABCD中,AB=4cm,BC=8cm,AC的垂直平分线EF分别交AD,BC于点E,F,垂足为点O. 已知:一次越野赛中,当小明跑了1600米时,小强跑了1400米.小明,小强此后所跑的路程y(米)与时间t(秒)之间的函数关系如图所示.
已知:一次越野赛中,当小明跑了1600米时,小强跑了1400米.小明,小强此后所跑的路程y(米)与时间t(秒)之间的函数关系如图所示.