题目内容
9. 如图,等边△ABC及其内切圆与外接圆构成的图形中,若外接圆的半径为3,则阴影部分的面积为( )
如图,等边△ABC及其内切圆与外接圆构成的图形中,若外接圆的半径为3,则阴影部分的面积为( )| A. | 2π | B. | 3π | C. | 4π | D. | 6π |
分析 阴影部分的面积等于圆心角是120°的扇形的面积,代入数值求出即可.
解答 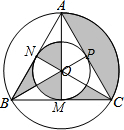 解:∵△ABC是等边三角形,大⊙O是△ABC的外切圆,
解:∵△ABC是等边三角形,大⊙O是△ABC的外切圆,
∴AO=OB=OC,
∵小⊙O是△ABC的内切圆,
∴OM=ON=OP,
∴∠AOC=120°,∠AON=∠BON=∠AOP=∠CON=60°,
BN=CM=AP=CP,
∴S阴影=S扇形AOC=$\frac{120•{π•3}^{2}}{360}$=3π.
故选B.
点评 本题考查了三角形的内切圆与内心,等边三角形的性质,扇形的面积计算,三角形的外切圆和外心,把各个阴影部分拼成一个扇形是解题的关键.

练习册系列答案
相关题目
19.如果代数式$\frac{\sqrt{-x}}{x+1}$有意义,则x的取值范围是( )
| A. | x≤0 | B. | x≠-1 | C. | x≤0且x≠-1 | D. | x>-1 |
20.某校九年级6个班合作学习小组的个数分别是:8,7,9,7,8,7,这组数据的众数和中位数分别是( )
| A. | 7和7.5 | B. | 7和8 | C. | 9和7.5 | D. | 7.5和7 |
4. 如图,在一次测绘活动中,某同学站在点A观测放置于B,C两处的标志物,数据显示点B在点A南偏东75°方向20米处,点C在点A南偏西15°方向20米处,则点B与点C的距离为20$\sqrt{2}$米.
如图,在一次测绘活动中,某同学站在点A观测放置于B,C两处的标志物,数据显示点B在点A南偏东75°方向20米处,点C在点A南偏西15°方向20米处,则点B与点C的距离为20$\sqrt{2}$米.
 如图,在一次测绘活动中,某同学站在点A观测放置于B,C两处的标志物,数据显示点B在点A南偏东75°方向20米处,点C在点A南偏西15°方向20米处,则点B与点C的距离为20$\sqrt{2}$米.
如图,在一次测绘活动中,某同学站在点A观测放置于B,C两处的标志物,数据显示点B在点A南偏东75°方向20米处,点C在点A南偏西15°方向20米处,则点B与点C的距离为20$\sqrt{2}$米.
18.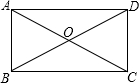 如图,矩形ABCD的对角线AC、BD相交于点O,AB=3,∠AOD=120°,则AD的长为( )
如图,矩形ABCD的对角线AC、BD相交于点O,AB=3,∠AOD=120°,则AD的长为( )
 如图,矩形ABCD的对角线AC、BD相交于点O,AB=3,∠AOD=120°,则AD的长为( )
如图,矩形ABCD的对角线AC、BD相交于点O,AB=3,∠AOD=120°,则AD的长为( )| A. | 3 | B. | 3$\sqrt{3}$ | C. | 6 | D. | 3$\sqrt{5}$ |
19.如图,用一张半径为24cm的扇形纸板制作一顶圆锥形帽子(接缝忽略不计),如果圆锥形帽子的底面半径为10cm,那么这张扇形纸板的面积是( )


| A. | 240πcm2 | B. | 480πcm2 | C. | 1200πcm2 | D. | 2400πcm2 |
 如图,将矩形ABCD沿AE折叠,点D恰好落在BC边上的点F处,若AB:AD=2:3,则tan∠AFB值是$\frac{2\sqrt{5}}{5}$.
如图,将矩形ABCD沿AE折叠,点D恰好落在BC边上的点F处,若AB:AD=2:3,则tan∠AFB值是$\frac{2\sqrt{5}}{5}$. 如图,分别过反比例函数y=$\frac{3}{x}$图象上的点P1(1,y1),P2(2,y2),…,Pn(n,yn),…作x轴的垂线,垂足分别为A1、A2、A3…An…连接A1P2,A2P3,…,An-1Pn,…再以A1P1,A1P2为一组邻边画一个平行四边形A1P1B1P2,以A2P2,A2P3为一组邻边画一个平行四边形A2P2B2P3,…此次类推,则点B10的纵坐标是$\frac{63}{110}$.
如图,分别过反比例函数y=$\frac{3}{x}$图象上的点P1(1,y1),P2(2,y2),…,Pn(n,yn),…作x轴的垂线,垂足分别为A1、A2、A3…An…连接A1P2,A2P3,…,An-1Pn,…再以A1P1,A1P2为一组邻边画一个平行四边形A1P1B1P2,以A2P2,A2P3为一组邻边画一个平行四边形A2P2B2P3,…此次类推,则点B10的纵坐标是$\frac{63}{110}$.