题目内容
3.等腰三角形底边上的高为腰的一半,则它的顶角为120°.分析 根据直角三角形的性质可求得等腰三角形的底角的度数,根据三角形内角和定理即可求得其顶角的度数.
解答 解:∵在直角△ABD中,AD=$\frac{1}{2}$AB,
∴∠B=30°,
∵AB=AC,
∴∠C=30°,
∴∠BAC=120°.
故答案为:120°.
点评 本题主要考查了等腰三角形的性质,直角三角形的性质及三角形内角和定理的综合运用,灵活运用定理、正确画出图形是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
13.在(-1)2015,|-1|3,-(-1)18,18这四个有理数中,负数共有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
11.抛物线y=ax2+bx+c与x轴的交点是(-3,0),(1,0),则这条抛物线的对称轴是( )
| A. | 直线x=-3 | B. | 直线x=-1 | C. | 直线x=0 | D. | 直线x=1 |
18. 如图,∠A=60°,∠B=80°,则∠1+∠2=( )
如图,∠A=60°,∠B=80°,则∠1+∠2=( )
 如图,∠A=60°,∠B=80°,则∠1+∠2=( )
如图,∠A=60°,∠B=80°,则∠1+∠2=( )| A. | 100° | B. | 120° | C. | 140° | D. | 150° |
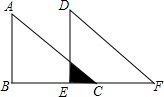 如图,等腰直角三角形ABC中,∠ABC=90°,AB=BC=4cm,将△ABC沿BC方向平移3cm后,得△DEF,则图中阴影部分的面积为$\frac{1}{2}$cm2.
如图,等腰直角三角形ABC中,∠ABC=90°,AB=BC=4cm,将△ABC沿BC方向平移3cm后,得△DEF,则图中阴影部分的面积为$\frac{1}{2}$cm2. 如图,等边三角形ABC中,BD是AC边上的中线,BD=BE,则∠EDA=15 度.
如图,等边三角形ABC中,BD是AC边上的中线,BD=BE,则∠EDA=15 度.