题目内容

5．已知a，b，c是△ABC的三条边，若方程（c-b）x2+2（b-a）x+a-b=0有两个相等实数根，那么，这个三角形是（　　）
A．等腰三角形B．等边三角形C．直角三角形D．等腰直角三角形

分析 根据判别式的意义得到△=4（b-a）2-4（c-b）（a-b）=0，再把作边因式分解得到a-b=0或a-c=0，于是可判断三角形为等腰三角形．

解答 解：根据题意得△=4（b-a）2-4（c-b）（a-b）=0，
所以（a-b）（a-b-c+b）=0，
即（a-b）（a-c）=0，
即a-b=0或a-c=0，
所以a=b或a=c，
所以三角形为等腰三角形．
故选A．

点评 本题考查了根的判别式：利用一元二次方程根的判别式（△=b2-4ac）判断方程的根的情况．

练习册系列答案
相关题目
15．如果记y=$\frac{{x}^{2}}{1+{x}^{2}}$=f（x），并且f（1）表示当x=1时y的值，即f（1）=$\frac{{1}^{2}}{1+{1}^{2}}$=$\frac{1}{2}$；f（$\frac{1}{2}$）表示当x=$\frac{1}{2}$时y的值，即f（$\frac{1}{2}$）=$\frac{（\frac{1}{2}）^{2}}{1+（\frac{1}{2}）^{2}}$=$\frac{1}{5}$．
（1）求f（3）=$\frac{9}{10}$；f（$\frac{1}{3}$）=$\frac{1}{10}$．
（2）猜想f（x）与f（$\frac{1}{x}$）的关系，并验证．
16．若a-b=3，x-y=2，则a2-2ab+b2-x+y=7．
13．某一个月的月历中成一竖列的连续三个日期的和是33，这三天分别是4，11，18．
20．某市出租车收费标准是：起步价7元（3千米以内），3千米后每千米收取1.8元，某乘客乘坐了x千米（x＞3）．
（1）请用含x的代数式表示他应该支付的车费（要求通过计算化简）．
（2）若该乘客乘坐了12千米，那他应该支付多少钱？
（3）如果一个乘客有40元，要到里程20千米的地方（不考虑其他因素），他的钱够支付吗？请说明理由．
10．若A（a1，b1），B（a2，b2）是反比例函数y=$\frac{1}{x}$（x＞0）图象上的两个点，且a1＜a2，则b1与b2的大小关系是（　　）
A．b1＞b2B．b1=b2C．b1＜b2D．大小不确定
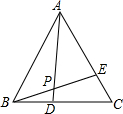17．如图，已知等边△ABC中，DC=EA，AD与BE相交于点P，求∠APB的度数．
14．比-3大-10的数是-13．
15．如图，一艘客轮沿东北方向OC行驶，在海上O处发现灯塔A在北偏西30°方向上，灯塔B在南偏东60°方向上．
（1）在图上画出射线OA、OB、OC，并在图上标出它们的方向角；
（2）求∠AOC和∠BOC的度数，由此你发现了什么？

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网