题目内容
6. 如图,AD为△ABC的高,BE为△ABC的角平分线,若∠EBA=32°,∠AEB=
如图,AD为△ABC的高,BE为△ABC的角平分线,若∠EBA=32°,∠AEB=70°.
(I)求∠CAD的度数;
(2)若点F为线段BC上任意一点,当△EFC为直角三角形时,则∠BEF的度数为58°或20°.
分析 (1)根据角平分线的定义、三角形内角和定理计算即可;
(2)分∠EFC=90°和∠FEC=90°两种情况解答即可.
解答 解:(1)∵BE为△ABC的角平分线,
∴∠CBE=∠EBA=32°,
∵∠AEB=∠CBE+∠C,
∴∠C=70°-32°=38°,
∵AD为△ABC的高,
∴∠ADC=90°,
∴∠CAD=90°-∠C=52°;
(2)当∠EFC=90°时,∠BEF=90°-∠CBE=58°,
当∠FEC=90°时,∠BEF=180°70°-90°=20°,
故答案为:58°或20°.
点评 本题考查的是三角形的内角和定理,掌握三角形内角和等于180°是解题的关键.

练习册系列答案
相关题目
5.化简a2÷b•$\frac{1}{b}$的结果是( )
| A. | a | B. | $\frac{{a}^{2}}{{b}^{2}}$ | C. | $\frac{a}{{b}^{2}}$ | D. | a2 |
 如图,小明的家D距离大树底部A是9米,一次台风过后,大树在离地面3米的点B处折断,顶端着地处点C在AD上,又知BC恰好等于CD.
如图,小明的家D距离大树底部A是9米,一次台风过后,大树在离地面3米的点B处折断,顶端着地处点C在AD上,又知BC恰好等于CD.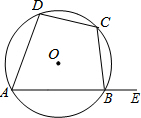 如图,四边形ABCD的四个顶点都在⊙O上,∠ADC=85°,在探究“四点共圆的条件”的活动中,知道∠ADC与∠ABC互补,若∠EBC是ABCD的一个外角,则∠EBC=85°.
如图,四边形ABCD的四个顶点都在⊙O上,∠ADC=85°,在探究“四点共圆的条件”的活动中,知道∠ADC与∠ABC互补,若∠EBC是ABCD的一个外角,则∠EBC=85°. 如图,求∠A+∠B+∠C+∠D+∠E+∠F+∠G的度数.
如图,求∠A+∠B+∠C+∠D+∠E+∠F+∠G的度数.