题目内容
18．
如图，求∠A+∠B+∠C+∠D+∠E+∠F+∠G的度数．
分析 根据四边形的内角和是360°，可求∠F+∠G+∠E+∠2=360°，∠1+∠3+∠C+∠D=360°．又由三角形的一个外角等于与它不相邻的两个内角的和，得∠1=∠A+∠B，而∠2+∠3=180°，从而求出所求的角的和．
解答 
解：在四边形EFGN中：∠F+∠G+∠E+∠2=360°，
在四边形NHCD中：∠1+∠3+∠C+∠D=360°．
∵∠1=∠A+∠B，∠2+∠3=180°，
∴∠A+∠B+∠C+∠D+∠E+∠F+∠G=360°+360°-180°=540°．
点评 本题考查三角形外角的性质及四边形的内角和定理，解答的关键是沟通外角和内角的关系．
练习册系列答案
各地期末复习特训卷系列答案
小博士期末闯关100分系列答案
相关题目
16．农业部门引进一批新麦种，在播种前做了五次发芽试验，目的是想了解一粒这样的麦种发芽情况，实验统计数据如下：
估计在与实验条件相同的情况下，种一粒这样的麦种发芽的概率约为0.98．
| 实验的麦种数/粒 | 500 | 500 | 500 | 500 | 500 |
| 发芽的麦种数/粒 | 492 | 487 | 491 | 493 | 489 |
| 发芽率/% | 98.40 | 97.40 | 98.20 | 98.60 | 97.80 |
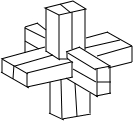鲁班锁是中国传统的智力玩具．起源于古代汉族建筑中首创的榫卯结构．这种三维的拼插器具内部的凹凸部分（即榫卯结构）啮合十分巧妙．外观看是严丝合缝的十字立方体，其上下、左右、前后完全对称．从外表上看，六根等长的正四棱柱体分成三组，经90°榫卯起来，如图，若正四棱柱体的高为6，底面正方形的边长为1，现将该鲁班锁放进一个球形容器内，则该球形容器的表面积的最小值为96．（容器壁的厚度忽略不计）
如图，AD为△ABC的高，BE为△ABC的角平分线，若∠EBA=32°，∠AEB=
如图所示是一个模具的横截面图，求∠A+∠B+∠C+∠D+∠E+∠F+∠G的值．
∠ACB=∠ADC=90°，AC=3，CD=2．当AB的长为$\frac{9\sqrt{5}}{5}$或$\frac{9}{2}$时，这两个直角三角形相似．
10．
如图，在正方形网格上有五个三角形，其中与△ABC全等（不包括本身）的三角形有（ ）
如图，在正方形网格上有五个三角形，其中与△ABC全等（不包括本身）的三角形有（ ）| A． | 4个 | B． | 3个 | C． | 2个 | D． | 1个 |
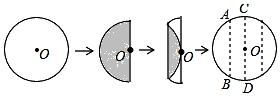把一张圆形纸片按如图方式折叠两次后展开，图中的虚线表示折痕，则弧$\widehat{BC}$的度数是150°．