题目内容
1.在等腰三角形ABC中,AB=AC,∠B=30°,D,E分别为边AB,AC上的动点,且DE∥BC,设BD=x,四边形BDCE的面积为S.若四边形DBCE的周长为60,则S关于x的函数表达式是S=-$\frac{1}{2}$x2+15x,四边形DBCE的面积最大值为$\frac{225}{2}$.分析 如图,过D作DF⊥BC于F,根据平行线等分线段定理得到CE=BD=x,根据直角三角形的性质得到DF=$\frac{1}{2}$BD=$\frac{1}{2}$x,根据梯形的面积公式即可得到结论.
解答  解:如图,过D作DF⊥BC于F,
解:如图,过D作DF⊥BC于F,
∵AB=AC,DE∥BC,
∴CE=BD=x,
∵∠B=30°,
∴DF=$\frac{1}{2}$BD=$\frac{1}{2}$x,
∵四边形DBCE的周长为60,
∴DE+BC=60-2x,
∴S=$\frac{1}{2}$(BC+DE)•DF=$\frac{1}{2}$(60-2x)$•\frac{1}{2}$x=-$\frac{1}{2}$x2+15x,
即S=-$\frac{1}{2}$(x-15)2+$\frac{225}{2}$,
∴四边形DBCE的面积最大值=$\frac{225}{2}$.
故答案为:S=-$\frac{1}{2}$x2+15x,$\frac{225}{2}$.
点评 本题考查了二次函数的应用,等腰三角形的性质,解直角三角形,图形面积的计算,正确的作出图形是解题的关键.

练习册系列答案
相关题目
19.下列是一元一次方程的是( )
| A. | $\frac{2}{x}$-3=0 | B. | x+5y=4 | C. | 2x+3 | D. | 5x+3=4 |
4.下列关系中,y不是x的函数关系的是( )
| A. | 长方形的长一定时,其面积y与宽x | |
| B. | 高速公路上匀速行驶的汽车,其行驶的路程y与行驶的时间x | |
| C. | y=|x| | |
| D. | |y|=x |
10. 如图,在正方形网格上有五个三角形,其中与△ABC全等(不包括本身)的三角形有( )
如图,在正方形网格上有五个三角形,其中与△ABC全等(不包括本身)的三角形有( )
 如图,在正方形网格上有五个三角形,其中与△ABC全等(不包括本身)的三角形有( )
如图,在正方形网格上有五个三角形,其中与△ABC全等(不包括本身)的三角形有( )| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
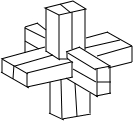 鲁班锁是中国传统的智力玩具.起源于古代汉族建筑中首创的榫卯结构.这种三维的拼插器具内部的凹凸部分(即榫卯结构)啮合十分巧妙.外观看是严丝合缝的十字立方体,其上下、左右、前后完全对称.从外表上看,六根等长的正四棱柱体分成三组,经90°榫卯起来,如图,若正四棱柱体的高为6,底面正方形的边长为1,现将该鲁班锁放进一个球形容器内,则该球形容器的表面积的最小值为96.(容器壁的厚度忽略不计)
鲁班锁是中国传统的智力玩具.起源于古代汉族建筑中首创的榫卯结构.这种三维的拼插器具内部的凹凸部分(即榫卯结构)啮合十分巧妙.外观看是严丝合缝的十字立方体,其上下、左右、前后完全对称.从外表上看,六根等长的正四棱柱体分成三组,经90°榫卯起来,如图,若正四棱柱体的高为6,底面正方形的边长为1,现将该鲁班锁放进一个球形容器内,则该球形容器的表面积的最小值为96.(容器壁的厚度忽略不计) 如图,AD为△ABC的高,BE为△ABC的角平分线,若∠EBA=32°,∠AEB=
如图,AD为△ABC的高,BE为△ABC的角平分线,若∠EBA=32°,∠AEB= 如图所示是一个模具的横截面图,求∠A+∠B+∠C+∠D+∠E+∠F+∠G的值.
如图所示是一个模具的横截面图,求∠A+∠B+∠C+∠D+∠E+∠F+∠G的值.