题目内容
2．
如图，小明的家D距离大树底部A是9米，一次台风过后，大树在离地面3米的点B处折断，顶端着地处点C在AD上，又知BC恰好等于CD．（1）请用直尺和圆规作出点C的位置（保留作图痕迹，不必写作法）；
（2）求大树折断前高度．
分析 （1）连结BD，作出BD的垂直平分线交AD于C，点C即为所求；
（2）根据垂直平分线的性质得到BC=CD，根据勾股定理求出BC的长，再由大树的高=BC+AB即可得出结论．
解答 解：（1）如图所示，点C即为所求；
（2）依题意有：
BC2=AC2+AB2，即BC2=（9-BC）2+32，
解得BC=5，
故大树的高=BC+AB=5+3=8米．
点评 本题考查的是勾股定理的应用，在应用勾股定理解决实际问题时勾股定理与方程的结合是解决实际问题常用的方法，关键是从题中抽象出勾股定理这一数学模型，画出准确的示意图．领会数形结合的思想的应用．
练习册系列答案
培优口算题卡系列答案
开心口算题卡系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
12．
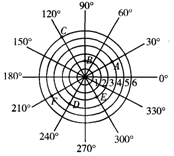如图，雷达探测器测得六个目标A，B，C，D，E，F出现按照规定的目标表示方法，目标E，F的位置表示为E（3，300°），F（5，210°），按照此方法在表示目标A，B，D，E的位置时，其中表示不正确的是（ ）
如图，雷达探测器测得六个目标A，B，C，D，E，F出现按照规定的目标表示方法，目标E，F的位置表示为E（3，300°），F（5，210°），按照此方法在表示目标A，B，D，E的位置时，其中表示不正确的是（ ）| A． | A（4，30°） | B． | B（2，90°） | C． | C（6，120°） | D． | D（3，240°） |
13．下列方程属于一元一次方程的是（ ）
| A． | $\frac{1}{x}$-1=0 | B． | 6x+1=3y | C． | 3m=2 | D． | 2y2-4y+1=0 |
10．从多边形的一个顶点出发向其余的顶点引对角线，将多边形分成10个三角形，则此多边形的边数为（ ）
| A． | 9 | B． | 11 | C． | 12 | D． | 10 |
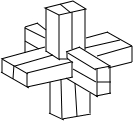鲁班锁是中国传统的智力玩具．起源于古代汉族建筑中首创的榫卯结构．这种三维的拼插器具内部的凹凸部分（即榫卯结构）啮合十分巧妙．外观看是严丝合缝的十字立方体，其上下、左右、前后完全对称．从外表上看，六根等长的正四棱柱体分成三组，经90°榫卯起来，如图，若正四棱柱体的高为6，底面正方形的边长为1，现将该鲁班锁放进一个球形容器内，则该球形容器的表面积的最小值为96．（容器壁的厚度忽略不计）
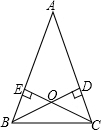如图，在△ABC中，AB=AC，BD、CE是腰AB、AC上的高，交于点O．
如图，AD为△ABC的高，BE为△ABC的角平分线，若∠EBA=32°，∠AEB=
∠ACB=∠ADC=90°，AC=3，CD=2．当AB的长为$\frac{9\sqrt{5}}{5}$或$\frac{9}{2}$时，这两个直角三角形相似．
4．下列四组数中不能构成直角三角形的一组是（ ）
| A． | 1，2，$\sqrt{6}$ | B． | 3，5，4 | C． | 5，12，13 | D． | 3，2，$\sqrt{13}$ |