题目内容
5.若y-4与x成正比例,且x=1时,y=8.(1)求y关于x的函数解析式:
(2)画出(1)中函数图象,若图象与x轴交于点A,与y轴交于点B,又知C(5,-1),求△ABC的面积.
分析 (1)设y-4=kx,即y=kx+4,将x、y的值代入求出k即可;
(2)根据解析式可得函数图象,再利用割补法求出面积即可.
解答 解:(1)根据题意,设y-4=kx,即y=kx+4,
将x=1、y=8代入,得:k+4=8,
解得:k=4,
∴y=4x+4;
(2)函数图象如下: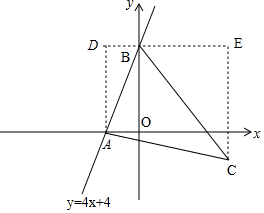
在y=4x+4中,当x=0时,y=4;
当y=0时,4x+4=0,
解得:x=-1,
∴点A的坐标为(-1,0),点B的坐标为(0,4),
由图可知,S△ABC=S梯形ADEC-S△ABD-S△BCE
=$\frac{1}{2}$×(4+5)×6-$\frac{1}{2}$×4×1-$\frac{1}{2}$×5×5
=12.5.
点评 本题主要考查待定系数法求函数解析式及割补法求面积,熟练掌握待定系数法求函数解析式是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15. 如图,边长为1的正方形ABCD顶点A(0,1),B(1,1);一抛物线y=ax2+bx+c过点M(-1,0)且顶点在正方形ABCD内部(包括在正方形的边上),则a的取值范围是( )
如图,边长为1的正方形ABCD顶点A(0,1),B(1,1);一抛物线y=ax2+bx+c过点M(-1,0)且顶点在正方形ABCD内部(包括在正方形的边上),则a的取值范围是( )
 如图,边长为1的正方形ABCD顶点A(0,1),B(1,1);一抛物线y=ax2+bx+c过点M(-1,0)且顶点在正方形ABCD内部(包括在正方形的边上),则a的取值范围是( )
如图,边长为1的正方形ABCD顶点A(0,1),B(1,1);一抛物线y=ax2+bx+c过点M(-1,0)且顶点在正方形ABCD内部(包括在正方形的边上),则a的取值范围是( )| A. | -2≤a≤-1 | B. | -2≤a≤-$\frac{1}{4}$ | C. | -1≤a≤-$\frac{1}{2}$ | D. | -1≤a≤-$\frac{1}{4}$ |
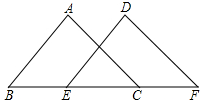 如图,点B、E、C、F在同一条直线上,∠A=∠D,AB∥DE,BE=CF,求证:AC∥DF.
如图,点B、E、C、F在同一条直线上,∠A=∠D,AB∥DE,BE=CF,求证:AC∥DF.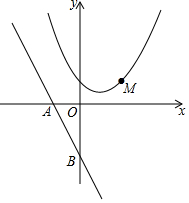 直线y=-$\frac{4}{3}$x-4与x轴交于点A,与y轴交于点B,抛物线y=x2-4x+5上的一点M(3,2).
直线y=-$\frac{4}{3}$x-4与x轴交于点A,与y轴交于点B,抛物线y=x2-4x+5上的一点M(3,2).