题目内容
1. 如图所示,⊙O是△ABC的内切圆,切点分别为E、F、D,且BC=a,AC=b,AB=c,试求AF、CF、BD的长.
如图所示,⊙O是△ABC的内切圆,切点分别为E、F、D,且BC=a,AC=b,AB=c,试求AF、CF、BD的长.
分析 根据切线长定理得出AE=AF,CF=CD,BC=BE,设AE=AF=x,则CF=CD=b-x,BD=BE=c-x,再由BD+CD=a即可得出x的值,进而可得出结论.
解答 解:∵⊙O是△ABC的内切圆,切点分别为E、F、D,
∴AE=AF,CF=CD,BC=BE.
∵BC=a,AC=b,AB=c,
∴设AE=AF=x,则CF=CD=b-x,BD=BE=c-x
∵BD+CD=a,
∴b-x+c-x=a,解得x=$\frac{b+c-a}{2}$,
∴AF=$\frac{b+c-a}{2}$,CF=b-$\frac{b+c-a}{2}$=$\frac{b-c+a}{2}$,BD=c-$\frac{b+c-a}{2}$=$\frac{c-b+a}{2}$.
点评 本题考查的是三角形的内切圆与内心,熟知切线长定理是解答此题的关键.

练习册系列答案
相关题目
12.某校组织七年级学生到距离学校6km的科技馆去参观,小胖同学因事没能乘上学校的包车,于是准备在校门口乘岀租车去科技馆,出租车收费标准如表:
(1)若出租车行驶的里程为3km,则要付车费多少元?;
(2)若出租车行驶的里程为x km(x>3),请用x的代数式表示车费y元;
(3)小胖同学身上仅有10元钱,够不够支付乘出租车到科技馆的车费?请说明理由.
| 里程(单位:km) | 收费(单位:元) |
| 3km以下(含3km) | 8.0 |
| 3km以上(每增加1km) | 1.80 |
(2)若出租车行驶的里程为x km(x>3),请用x的代数式表示车费y元;
(3)小胖同学身上仅有10元钱,够不够支付乘出租车到科技馆的车费?请说明理由.
9.抛物线y=ax2-2ax+c经过点A(2,4),若其顶点在第四象限,则a的取值范围为( )
| A. | a>4 | B. | 0<a<4 | C. | a>2 | D. | 0<a<2 |
10.下列抛物线顶点坐标为(-2,3)的是( )
| A. | y=-2(x+2)2+3 | B. | y=-3(x-2)2+3 | C. | y=-5(x+2)2-3 | D. | y=-5(x-2)2-3 |
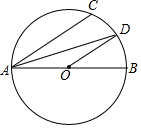 如图,AB为⊙O的直径,点C为半圆上一点,AD平分∠CAB交⊙O于点D
如图,AB为⊙O的直径,点C为半圆上一点,AD平分∠CAB交⊙O于点D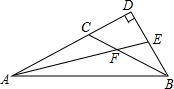 如图,在△ABC中,∠CAB=∠ABC=$\frac{1}{4}$∠ACB,AF是∠CAB的平分线,延长AF交AC边上的高BD于点E,求∠AEB的度数.
如图,在△ABC中,∠CAB=∠ABC=$\frac{1}{4}$∠ACB,AF是∠CAB的平分线,延长AF交AC边上的高BD于点E,求∠AEB的度数.