题目内容
9．抛物线y=ax2-2ax+c经过点A（2，4），若其顶点在第四象限，则a的取值范围为（ ）| A． | a＞4 | B． | 0＜a＜4 | C． | a＞2 | D． | 0＜a＜2 |
分析 把A点坐标代入可得到a、c的关系式，再由顶点式可求得其顶点坐标，利用条件可得到关于a的不等式，可求得a的取值范围．
解答 解：
∵抛物线y=ax2-2ax+c经过点A（2，4），
∴4=4a-4a+c，解得c=4，
∴y=ax2-2ax+4=a（x-1）2+4-a，
∴顶点坐标为（1，4-a），
∵顶点坐标在第四象限，
∴4-a＜0，解得a＞4，
故选A．
点评 本题主要考查二次函数的性质，掌握抛物线的顶点式是解题的关键，即在y=a（x-h）2+k中，顶点坐标为（h，k），对称轴为x=h．
练习册系列答案
高中必刷题系列答案
相关题目
19．下列实数中，无理数是（ ）
| A． | -$\frac{5}{2}$ | B． | $\frac{{\sqrt{2}}}{2}$ | C． | $\sqrt{9}$ | D． | |-2| |
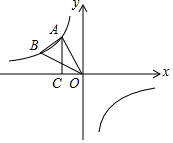如图，点A，点B在反比例函数y=$\frac{k}{x}$的图象上，且点A，点B的横坐标分别为a，2a（a＜0），AC⊥x轴于点C，且S△AOC=2．
如图所示，将直径AB=6的半圆绕着点A逆时针旋转30°，此时点B落到点C处，图中阴影部分的面积是3π．
如图所示，⊙O是△ABC的内切圆，切点分别为E、F、D，且BC=a，AC=b，AB=c，试求AF、CF、BD的长．