题目内容
19.将图1中线段AD上一点E(点A、D除外)向下拖动,依次可得图2、图3、图4,分别探究图2、图3、图4中∠A、∠B、∠C、∠D、∠E(∠AED)之间有什么关系?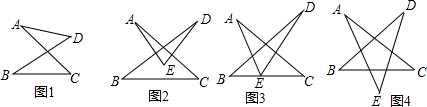
分析 连结AD,AC与BD相交于点O,如图,在△AOD和△BOC中,根据三角形内角和定理得到∠OAD+∠ODA+∠AOD=180°,∠B+∠C+∠BOC=180°,而由对顶角相等得∠AOD=∠BOC,则∠OAD+∠ODA=∠B+∠C,再在△ADE中,由三角形内角和定理得∠OAD+∠ODA=180°-(∠A+∠D+∠E),所以180°-(∠A+∠D+∠E)=∠B+∠C,于是整理可得∠A+∠B+∠C+∠D+∠E=180°.
解答 解: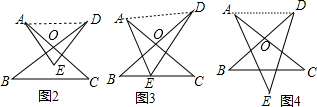 连结AD,AC与BD相交于点O,如图,
连结AD,AC与BD相交于点O,如图,
在△AOD和△BOC中,∵∠OAD+∠ODA+∠AOD=180°,
∠B+∠C+∠BOC=180°,
而∠AOD=∠BOC,
∴∠OAD+∠ODA=∠B+∠C,
在△ADE中,∵∠OAD+∠ODA+∠A+∠D+∠E=180°,
∴∠OAD+∠ODA=180°-(∠A+∠D+∠E),
∴180°-(∠A+∠D+∠E)=∠B+∠C,
∴∠A+∠B+∠C+∠D+∠E=180°.
点评 本题考查了三角形内角和定理:三角形内角和是180°.准确识别图形,即在哪个三角形中运用内角和定理是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
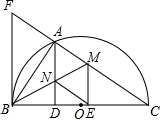 如图,以BC为直径,以O为圆心的半圆交△CFB的边CF于点A,BM平分∠ABC交AC于点M,AD⊥BC于点D,AD交BM于点N,ME⊥BC于点E,BC2=CF•AC,cos∠ABD=$\frac{3}{5}$,AD=12.
如图,以BC为直径,以O为圆心的半圆交△CFB的边CF于点A,BM平分∠ABC交AC于点M,AD⊥BC于点D,AD交BM于点N,ME⊥BC于点E,BC2=CF•AC,cos∠ABD=$\frac{3}{5}$,AD=12. 小李家用40m长的篱笆围成一个一边靠墙(墙足够长)的矩形菜园,如图.
小李家用40m长的篱笆围成一个一边靠墙(墙足够长)的矩形菜园,如图.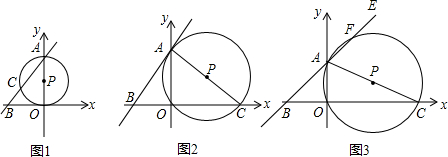
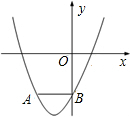 如图,已知二次函数y=x2+bx+c(c≠0)的图象经过点A(-2,m)(m<0),与y轴交于点B,AB∥x轴,且AB=OB.
如图,已知二次函数y=x2+bx+c(c≠0)的图象经过点A(-2,m)(m<0),与y轴交于点B,AB∥x轴,且AB=OB.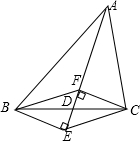 如图,AD是△ABC的中线,CF、BE分别垂直于AD,垂足分别为F、E,则四边形BECF是平行四边形,理由是一组对边平行且相等的四边形是平行四边形.
如图,AD是△ABC的中线,CF、BE分别垂直于AD,垂足分别为F、E,则四边形BECF是平行四边形,理由是一组对边平行且相等的四边形是平行四边形.