题目内容
12.已知$\frac{a}{b}$=$\frac{c}{d}$=$\frac{e}{f}$=$\frac{2}{3}$(b+d+f≠0),求$\frac{a+c+e}{b+d+f}$的值.分析 根据等比性质,可得答案.
解答 解:由$\frac{a}{b}$=$\frac{c}{d}$=$\frac{e}{f}$=$\frac{2}{3}$(b+d+f≠0),得
$\frac{a+c+e}{b+d+f}$=$\frac{2}{3}$.
点评 本题考查了比例的性质,利用了等比性质:$\frac{a}{b}$=$\frac{c}{d}$⇒$\frac{a+c}{b+d}$=$\frac{a}{b}$.

练习册系列答案
相关题目
20. 如图,点O是两个同心圆的圆心,大圆半径OA,OB交小圆于点C,D.下列结论中正确的个数有( )
如图,点O是两个同心圆的圆心,大圆半径OA,OB交小圆于点C,D.下列结论中正确的个数有( )
①∠OCD=∠OAB;②AB=CD;③$\widehat{AB}$=$\widehat{CD}$.
 如图,点O是两个同心圆的圆心,大圆半径OA,OB交小圆于点C,D.下列结论中正确的个数有( )
如图,点O是两个同心圆的圆心,大圆半径OA,OB交小圆于点C,D.下列结论中正确的个数有( )①∠OCD=∠OAB;②AB=CD;③$\widehat{AB}$=$\widehat{CD}$.
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
17.已知一个直角三角形的两条边长恰好是方程x2-5x+6=0的两根,则它的第三条边长为( )
| A. | $\sqrt{13}$ | B. | 13 | C. | $\sqrt{13}$或$\sqrt{5}$ | D. | $\sqrt{13}$或3 |
 用4块大小相同的正方形硬纸片拼成一个大正方形(如图).小明在2m外投掷飞镖,假设飞镖击中一块小正方形是等可能的(击中小正方形边界线或没有击中大正方形,则重投1次).
用4块大小相同的正方形硬纸片拼成一个大正方形(如图).小明在2m外投掷飞镖,假设飞镖击中一块小正方形是等可能的(击中小正方形边界线或没有击中大正方形,则重投1次). 的概率.
的概率.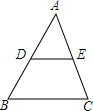 如图,△ABC中,DE∥BC,AD=6,AC=8,BD=AE,求BD的长.
如图,△ABC中,DE∥BC,AD=6,AC=8,BD=AE,求BD的长.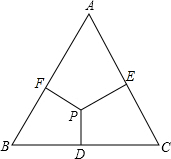 如图,P为正三角形ABC内任一点,PD⊥BC,PE⊥CA,PF⊥AB,则$\frac{PD+PE+PF}{BD+CE+AF}$=$\frac{\sqrt{3}}{3}$.
如图,P为正三角形ABC内任一点,PD⊥BC,PE⊥CA,PF⊥AB,则$\frac{PD+PE+PF}{BD+CE+AF}$=$\frac{\sqrt{3}}{3}$. 如图,在?ABCD中,A、E、F共线,B、C、F共线,则与△FCE相似的三角形有2个.
如图,在?ABCD中,A、E、F共线,B、C、F共线,则与△FCE相似的三角形有2个.