题目内容
已知
=
，
=
，求x：y：z．
| x |
| y |
| a+b |
| a-b |
| y |
| z |
| a+b |
| a-b |
考点：比例的性质
专题：
分析：根据比例式设y=k（a+b）（a-b），则x=k（a+b）2，z=k（a-b）2，再表示出x：y：z=k（a+b）2：k（a+b）（a-b）：k（a-b）2，化简即可．
解答：解：∵
=
，
=
，
∴设y=k（a+b）（a-b），则x=k（a+b）2，z=k（a-b）2，
则x：y：z
=k（a+b）2：k（a+b）（a-b）：k（a-b）2
=（a+b）2：（a+b）（a-b）：（a-b）2．
| x |
| y |
| a+b |
| a-b |
| y |
| z |
| a+b |
| a-b |
∴设y=k（a+b）（a-b），则x=k（a+b）2，z=k（a-b）2，
则x：y：z
=k（a+b）2：k（a+b）（a-b）：k（a-b）2
=（a+b）2：（a+b）（a-b）：（a-b）2．
点评：此题主要考查了比例的性质，关键是正确设y=k（a+b）（a-b），然后表示出x、z．
练习册系列答案
相关题目
正方形ABCD的边长为4，请你建立适当的平面直角坐标系，写出各个顶点的坐标．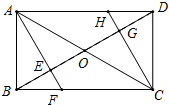
如图，矩形ABCD中，O是两条对角线的交点，AF垂直平分线段OB，垂足为E，CH垂直平分线段OD，垂足为G．求证：
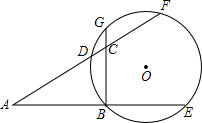已知在Rt△ABC中，∠ABC=90°，O为△ABC中∠B和∠C的外角平分线的交点，以O为圆心，OB为半径的⊙O与△ABC的三边所在的直线交于D、E、F、G．
已知在△ABC中，∠B=∠C，BD=CE，求证：DE∥BC．
若将后面7月份的日历接在6月份的下面，再将8月份的接在7月份的下面，将8月接在7月下，能用3×3的长方形框圈出9个数的和为120吗？下列二次根式中属于最简二次根式的是（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|