题目内容
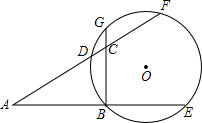 已知在Rt△ABC中,∠ABC=90°,O为△ABC中∠B和∠C的外角平分线的交点,以O为圆心,OB为半径的⊙O与△ABC的三边所在的直线交于D、E、F、G.
已知在Rt△ABC中,∠ABC=90°,O为△ABC中∠B和∠C的外角平分线的交点,以O为圆心,OB为半径的⊙O与△ABC的三边所在的直线交于D、E、F、G.(1)证明:BE=BG=DF;
(2)若AE=16,CG=2,求△ABC的周长.
考点:垂径定理,角平分线的性质,勾股定理
专题:
分析:(1)作OM⊥DF,ON⊥BG,OK⊥BE,根据角平分线的性质判断出OM=ON=OK,从而得到BE=BG=DF.
(2)连接OC,OA.易得,△OMC≌△ONC,△OMA≌△OKA,可知,CD=CG=2,AM=AK,得到AB=AD,
根据勾股定理求出AB的长即可解答.
(2)连接OC,OA.易得,△OMC≌△ONC,△OMA≌△OKA,可知,CD=CG=2,AM=AK,得到AB=AD,
根据勾股定理求出AB的长即可解答.
解答: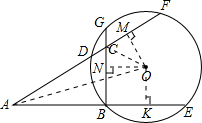 解:(1)作OM⊥DF,ON⊥BG,OK⊥BE,
解:(1)作OM⊥DF,ON⊥BG,OK⊥BE,
∵O为△ABC中∠B的外角平分线的交点,
∴OK=ON,
O为△ABC中∠C的外角平分线的交点,
∴OK=ON,
∴(2)连接OC,OA.
易得,△OMC≌△ONC,△OMA≌△OKA,
可知,CD=CG=2,AM=AK,
∵DM=BK,
∴AB=AD,
设AB=x,则CB=16-2-x=14-x,AC=2+x,
在Rt△ABG中,(x+2)2=x2+(14-x)2,
解得x1=24(舍去),x2=8.
可得△ABC的周长为16+8=24.
 解:(1)作OM⊥DF,ON⊥BG,OK⊥BE,
解:(1)作OM⊥DF,ON⊥BG,OK⊥BE,∵O为△ABC中∠B的外角平分线的交点,
∴OK=ON,
O为△ABC中∠C的外角平分线的交点,
∴OK=ON,
∴(2)连接OC,OA.
易得,△OMC≌△ONC,△OMA≌△OKA,
可知,CD=CG=2,AM=AK,
∵DM=BK,
∴AB=AD,
设AB=x,则CB=16-2-x=14-x,AC=2+x,
在Rt△ABG中,(x+2)2=x2+(14-x)2,
解得x1=24(舍去),x2=8.
可得△ABC的周长为16+8=24.
点评:本题考查了垂径定理、弦与弦心距的关系、勾股定理、角平分线的性质等,要综合运用,且要注意整体思想的运用.

练习册系列答案
相关题目
 如图,在平面直角坐标系中,四边形MNPO的顶点P的坐标是(3,4),且OM=OP,则顶点M的坐标是( )
如图,在平面直角坐标系中,四边形MNPO的顶点P的坐标是(3,4),且OM=OP,则顶点M的坐标是( )| A、(3,0) |
| B、(4,0) |
| C、(5,0) |
| D、(6,0) |
若方程ax2+bx+c=0的两个根是-3和1,那么二次函数y=ax2+bx+c的图象的对称轴是直线( )
| A、x=-3 | B、x=-2 |
| C、x=-1 | D、x=1 |
 如图,AB、CD的两条互相垂直的直径,点O1、O2、O3、O4分别是OA、OB、OC、OD的中点.若⊙O的半径是2,求阴影部分的面积.
如图,AB、CD的两条互相垂直的直径,点O1、O2、O3、O4分别是OA、OB、OC、OD的中点.若⊙O的半径是2,求阴影部分的面积.