题目内容
1.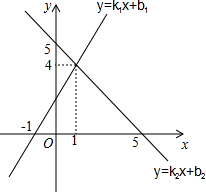 已知函数y=k1x+b1与函数y=k2x+b2的图象如图所示,则方程组$\left\{\begin{array}{l}{{k}_{1}x+{b}_{1}-y=0}\\{{k}_{2}x+{b}_{2}-y=0}\end{array}\right.$的解为( )
已知函数y=k1x+b1与函数y=k2x+b2的图象如图所示,则方程组$\left\{\begin{array}{l}{{k}_{1}x+{b}_{1}-y=0}\\{{k}_{2}x+{b}_{2}-y=0}\end{array}\right.$的解为( )| A. | $\left\{\begin{array}{l}{x=-1}\\{y=2}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=-1}\\{y=5}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=1}\\{y=4}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=5}\\{y=5}\end{array}\right.$ |
分析 根据任何一个一次函数都可以化为一个二元一次方程,再根据两个函数交点就是二元一次方程组的解可直接得到答案.
解答 解:∵函数y=k1x+b1与函数y=k2x+b2的图象交于点(1,4),
∴二元一次方程组$\left\{\begin{array}{l}{{k}_{1}x+{b}_{1}-y=0}\\{{k}_{2}x+{b}_{2}-y=0}\end{array}\right.$的解为$\left\{\begin{array}{l}{x=1}\\{y=4}\end{array}\right.$,
故选C.
点评 本题主要考查了一次函数与二元一次方程(组)的关系,比较简单,熟悉交点坐标就是方程组的解是解题的关键.

练习册系列答案
 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案
相关题目
9.若抛物线y=x2-bx+9的顶点在x轴的负半轴上,则b的值为( )
| A. | ±3 | B. | 6 | C. | -6 | D. | ±6 |
16.甲、乙两地相距270千米,从甲地开出一辆快车,速度为120千米/时,从乙地开出一辆慢车,速度为75千米/时,如果两车相向而行,慢车先开出1小时后,快车开出,那么再经过多长时间两车相遇?若设再经过x小时两车相遇,则根据题意列方程为( )
| A. | 75×1+(120-75)x=270 | B. | 75×1+(120+75)x=270 | ||
| C. | 120(x-1)+75x=270 | D. | 120×1+(120+75)x=270 |
6.己知代数式2y2+3y+7的值是8,则代数式4y2+6y-9的值是( )
| A. | 2 | B. | 17 | C. | 7 | D. | -7 |
 已知抛物线y=$\frac{1}{2}$x2-4x+c的顶点为D,与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C(0,6),连接BC、CD、BD.
已知抛物线y=$\frac{1}{2}$x2-4x+c的顶点为D,与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C(0,6),连接BC、CD、BD.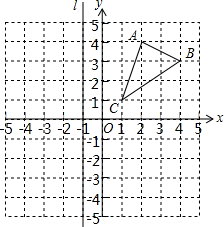 如图,已知△ABC的三个顶点的坐标为:A(2,4),B(4,3),C(1,1),直线l过点(-1,0)且平行于y轴.
如图,已知△ABC的三个顶点的坐标为:A(2,4),B(4,3),C(1,1),直线l过点(-1,0)且平行于y轴.