题目内容
12.计算:$|{\sqrt{3}-2}|+{({-\frac{1}{2}})^0}+\frac{2}{{\sqrt{3}}}-\sqrt{48}$+4sin60°.分析 根据绝对值、零指数幂的意义和特殊角的三角函数值得到原式=2-$\sqrt{3}$+1+$\frac{2\sqrt{3}}{3}$-4$\sqrt{3}$+4×$\frac{\sqrt{3}}{2}$,然后合并即可.
解答 解:原式=2-$\sqrt{3}$+1+$\frac{2\sqrt{3}}{3}$-4$\sqrt{3}$+4×$\frac{\sqrt{3}}{2}$
=2-$\sqrt{3}$+1+$\frac{2\sqrt{3}}{3}$-4$\sqrt{3}$+2$\sqrt{3}$
=3-$\frac{7\sqrt{3}}{3}$.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.也考查了零指数幂与特殊角的三角函数值.

练习册系列答案
 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
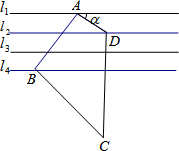 如图,已知直线l1∥l2∥l3∥l4,相邻两条平行直线间的距离都相等,如果直角梯形ABCD的三个顶点在平行直线上,∠ABC=90°且AB=2AD,则tanα=$\frac{2}{3}$.
如图,已知直线l1∥l2∥l3∥l4,相邻两条平行直线间的距离都相等,如果直角梯形ABCD的三个顶点在平行直线上,∠ABC=90°且AB=2AD,则tanα=$\frac{2}{3}$. 如图,若∠1+∠3=180°,能否得出AB∥CD?为什么?
如图,若∠1+∠3=180°,能否得出AB∥CD?为什么?
