Question

3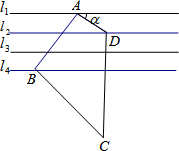．如图，已知直线l₁∥l₂∥l₃∥l₄，相邻两条平行直线间的距离都相等，如果直角梯形ABCD的三个顶点在平行直线上，∠ABC=90°且AB=2AD，则tanα=$\frac{2}{3}$．

Answer 1

分析 作AE⊥l₄，垂足为E，交l₂于点F，利用三角形相似的判定求出△ABE∽△DAF，得出$\frac{AB}{AD}$=$\frac{AE}{DF}$=2，假设AE=3y，DF=$\frac{3}{2}$y，AF=y，即可得出∠α的正切值．

解答 解：如图，

作AE⊥l₄，垂足为E，交l₂于点F，
∵直线l₁∥l₂∥l₃∥l₄，相邻两条平行直线间的距离都相等，直角梯形ABCD的三个顶点在平行直线上，∠ABC=90°，
∴∠BAE+∠EAD=90°，∠α+∠DAF=90°，
∴∠α=∠BAE，∠AEB=∠AFD，
∴△ABE∽△DAF，
∴出$\frac{AB}{AD}$=$\frac{AE}{DF}$，
∵AB=2AD，
∴$\frac{AB}{AD}$=2，
假设AE=3y，
∴DF=$\frac{3}{2}$y，AF=y，
∴tanα=$\frac{AF}{DF}$=$\frac{2}{3}$．
故答案为：$\frac{2}{3}$．

点评 此题主要考查了相似三角形的判定与性质，锐角三角函数的定义以及直角梯形的性质以及平行线分线段成比例定理，作出垂足利用相似三角形性质求出AF与DF是解决问题的关键．