题目内容
13．计算或化简：（1）22-（$\frac{1}{2}$+π）0-32÷33
（2）（x-2y）（x+y）-2y（x-2y）
分析 （1）根据零指数幂的意义，同底数幂的运算法则即可求出答案．
（2）根据整式的运算法则即可求出答案．
解答 解：（1）原式=4-1-$\frac{1}{3}$=$\frac{8}{3}$
（2）原式=（x-2y）（x+y-2y）
=（x-2y）（x-y）
=x2-3xy+2y2
点评 本题考查学生的运算能力，解题的关键是熟练运用运算法则，本题属于基础题型．
练习册系列答案
黄冈小状元解决问题天天练系列答案
三点一测快乐周计划系列答案
相关题目
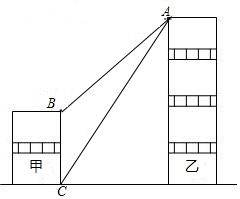小颖站在自家阳台的A处用测角仪观察对面的商场，如图，在A处测得商场楼顶B点的俯角为45°，商场楼底C点的俯角为60°，若商场高17.6米，小颖家所在楼房每层楼的平均高度为3米，则小颖家住在几楼？小颖家与商场相距多少米？（结果保留整数，参考数据：$\sqrt{3}$≈1.732，$\sqrt{2}$≈1.414）
8．
某批发部队外批发一种小商品，每个售价m元，如果一次购买100分以上，超过100个的部分售价打8折，付款金额y（元）与购买数量x（个）之间的关系如图所示，该批发部老板将某一天的销售情况绘制成如图所示的表格．
（1）求出y与x之间的函数表达式；
（2）m=5，a=300，b=900，c=350．
（3）若该小商品的进价为2元/个，请求出该批发部这一天所获得的利润．
某批发部队外批发一种小商品，每个售价m元，如果一次购买100分以上，超过100个的部分售价打8折，付款金额y（元）与购买数量x（个）之间的关系如图所示，该批发部老板将某一天的销售情况绘制成如图所示的表格．| 购买数量x（个） | 60 | 100 | 120 | 200 | c |
| 付款金额y（元） | a | 500 | 580 | b | 1500 |
（2）m=5，a=300，b=900，c=350．
（3）若该小商品的进价为2元/个，请求出该批发部这一天所获得的利润．
如图，数轴上A、B两点表示的数分别为$\sqrt{2}$和6.3，则A、B两点之间表示整数的点共有5个．