题目内容
7.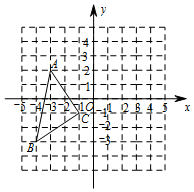 如图,(1)画出△ABC先向右平移4个单位,再向上平移1个单位后的图形△A'B'C';
如图,(1)画出△ABC先向右平移4个单位,再向上平移1个单位后的图形△A'B'C';(2)求直线A'C'的解析式;
(3)求△ABC中AB边上的高.
分析 (1)根据三角形平移的性质画出平移后的△A′B′C′即可;
(2)利用待定系数法求出直线A′C′的解析式即可;
(3)先根据勾股定理的逆定理判断出△ABC的形状,进而可得出结论.
解答 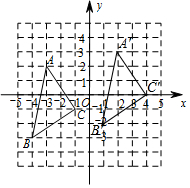 解:(1)如图,△A′B′C′即为所求;
解:(1)如图,△A′B′C′即为所求;
(2)设直线A′C′的解析式为y=kx+b(k≠0),
∵A′(2,3),C′(4,0),
∴$\left\{\begin{array}{l}{2k+b=3}\\{4k+b=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=-\frac{3}{2}}\\{b=\frac{9}{2}}\end{array}\right.$,
∴直线A′C′的解析式为:y=-$\frac{3}{2}$x+$\frac{9}{2}$;
(3)∵AB2=12+52=26,AC2=22+32=13,BC2=22+32=13,
∴△ABC是等腰直角三角形,
∴△ABC中AB边上的高=$\frac{\sqrt{13}×\sqrt{13}}{\sqrt{26}}$=$\frac{\sqrt{26}}{2}$.
点评 本题考查的是作图-平移变换及勾股定理的逆定理,熟知图形平移不变性的性质是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17. 为了解国家提倡的“阳光体育运动”的实施情况,将某校中的40名学生一周的体育锻炼时间绘制成了如图所示的条形统计图,根据统计图提供的数据,该校40名同学一周参加体育锻炼时间的众数与中位数分别是( )
为了解国家提倡的“阳光体育运动”的实施情况,将某校中的40名学生一周的体育锻炼时间绘制成了如图所示的条形统计图,根据统计图提供的数据,该校40名同学一周参加体育锻炼时间的众数与中位数分别是( )
 为了解国家提倡的“阳光体育运动”的实施情况,将某校中的40名学生一周的体育锻炼时间绘制成了如图所示的条形统计图,根据统计图提供的数据,该校40名同学一周参加体育锻炼时间的众数与中位数分别是( )
为了解国家提倡的“阳光体育运动”的实施情况,将某校中的40名学生一周的体育锻炼时间绘制成了如图所示的条形统计图,根据统计图提供的数据,该校40名同学一周参加体育锻炼时间的众数与中位数分别是( )| A. | 8,8 | B. | 8,9 | C. | 9,8 | D. | 10,9 |
12.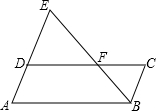 如图,点F是?ABCD的边CD上一点,直线BF交AD的延长线于点E,则下列结论错误的是( )
如图,点F是?ABCD的边CD上一点,直线BF交AD的延长线于点E,则下列结论错误的是( )
 如图,点F是?ABCD的边CD上一点,直线BF交AD的延长线于点E,则下列结论错误的是( )
如图,点F是?ABCD的边CD上一点,直线BF交AD的延长线于点E,则下列结论错误的是( )| A. | $\frac{ED}{EA}$=$\frac{DF}{AB}$ | B. | $\frac{DE}{CB}$=$\frac{EF}{FB}$ | C. | $\frac{BF}{BE}$=$\frac{BC}{AE}$ | D. | $\frac{BC}{DE}$=$\frac{BF}{BE}$ |
16.2015年11月,“喜迎G20•杭州毅行大会”在杭州市民中心盛大开幕,本次毅行大会参与总人数超过42000人,用科学记数法表示42000应为( )
| A. | 42×103 | B. | 4.2×105 | C. | 0.42×105 | D. | 4.2×104 |
 如图,∠MON=30°,且OP平分∠MON,过点P作PQ∥OM交ON于点Q.若点P到OM的距离为2,则OQ的长为( )
如图,∠MON=30°,且OP平分∠MON,过点P作PQ∥OM交ON于点Q.若点P到OM的距离为2,则OQ的长为( ) 从正面和左面看到长方体的图形如图所示(单位:cm),则从其上面看到图形的面积是12cm2.
从正面和左面看到长方体的图形如图所示(单位:cm),则从其上面看到图形的面积是12cm2.