题目内容
20．为庆祝交通大学建校120周年，我校特别推出校庆纪念卡片，卡片有两种，一种卡片正面印着交通大学的校训，另一种卡片正面印着交通大学的校徽，两种卡片除此之外完全相同．现将3张校训卡和4张校徽正面向下放置在桌面上，随机翻出4张卡片．则下列事件是必然事件的是（ ）| A． | 至少有一张是校训卡 | B． | 至少有一张是校徽卡 | ||
| C． | 翻出的卡既有校训卡又有校徽卡 | D． | 发出的卡片只有一种类型 |
分析 根据事件发生的可能性大小判断相应事件的类型即可．
解答 解：至少有一张是校训卡是随机事件；
至少有一张是校徽卡是必然事件；
翻出的卡既有校训卡又有校徽卡是随机事件；
发出的卡片只有一种类型是随机事件，
故选：B．
点评 本题考查的是必然事件、不可能事件、随机事件的概念．必然事件指在一定条件下，一定发生的事件．不可能事件是指在一定条件下，一定不发生的事件，不确定事件即随机事件是指在一定条件下，可能发生也可能不发生的事件．
练习册系列答案
相关题目
11．
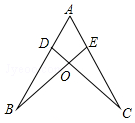如图，点D，E分别在线段AB，AC上，CD与BE相交于O点，有下列条件：①AB=AC；②DC=BE；③∠B=∠C，从中选择两个条件判定△ABE≌△ACD，是真命题的个数为（ ）
如图，点D，E分别在线段AB，AC上，CD与BE相交于O点，有下列条件：①AB=AC；②DC=BE；③∠B=∠C，从中选择两个条件判定△ABE≌△ACD，是真命题的个数为（ ）| A． | 0个 | B． | 1个 | C． | 2个 | D． | 3个 |
8．
如图，哪一个图形是左面正方体的展开图（ ）
如图，哪一个图形是左面正方体的展开图（ ）| A． |  | B． |  | C． |  | D． |  |
15．下列计算结果正确的是（ ）
| A． | 2+$\sqrt{5}$=2$\sqrt{5}$ | B． | $\sqrt{6}$÷$\sqrt{2}$=$\sqrt{3}$ | C． | （-2a2）3=-6a6 | D． | （x+1）2=x2+1 |
5．
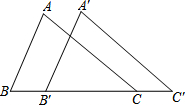如图，在△ABC中，AB=8，BC=12，∠B=60°，将△ABC沿着射线BC的方向平移4个单位后，得到△A'B'C'，连接AC，则△A'B'C的面积是（ ）
如图，在△ABC中，AB=8，BC=12，∠B=60°，将△ABC沿着射线BC的方向平移4个单位后，得到△A'B'C'，连接AC，则△A'B'C的面积是（ ）| A． | 16 | B． | $4\sqrt{3}$ | C． | $16\sqrt{3}$ | D． | $32\sqrt{3}$ |
12．若分式$\frac{x+2}{x-2}$的值为0，则x的取值应满足是（ ）
| A． | x=-2 | B． | x≠-2 | C． | x=2 | D． | x≠2 |
9．有一个正方体，6个面上分别标有1～6这6个整数，投掷这个正方体一次，则出现向上一面的数字为偶数的概率是（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{1}{3}$ | C． | $\frac{1}{4}$ | D． | $\frac{1}{6}$ |
10．已知一个等腰三角形两边长之比为1：4，周长为18，则这个等腰三角形底边长为（ ）
| A． | 2 | B． | 6 | C． | 8 | D． | 2或8 |