题目内容
15.程大位《直指算法统宗》:一百馒头一百僧,大僧三个更无争,小僧三人分一个,大小和尚得几丁.意思是:有100个和尚分100个馒头,如果大和尚1人分3个,小和尚3人分1个,正好分完.试问大、小和尚各多少人?设大和尚有x人,依题意列方程得3x+$\frac{100-x}{3}$=100.分析 根据100个和尚分100个馒头,正好分完.大和尚一人分3个,小和尚3人分一个得到等量关系为:大和尚的人数+小和尚的人数=100,大和尚分得的馒头数+小和尚分得的馒头数=100,依此列出方程即可.
解答 解:设大和尚有x人,则小和尚有(100-x)人,
根据题意得:3x+$\frac{100-x}{3}$=100;
故答案为3x+$\frac{100-x}{3}$=100.
点评 本题考查了由实际问题抽象出一元一次方程,关键以和尚数和馒头数作为等量关系列出方程.

练习册系列答案
相关题目
10.双曲线y=$\frac{1-k}{x}$与直线y=x没有交点,则k的取值范围是( )
| A. | k<1 | B. | k>1 | C. | k<-1 | D. | k>-1 |
20.已知m是关于x的方程x2-2x-3=0的一个根,则2m2-4m的值为( )
| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
4.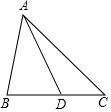 如图,△ABC中,点D在线段BC上,且△ABC∽△DBA,则下列结论一定正确的是( )
如图,△ABC中,点D在线段BC上,且△ABC∽△DBA,则下列结论一定正确的是( )
 如图,△ABC中,点D在线段BC上,且△ABC∽△DBA,则下列结论一定正确的是( )
如图,△ABC中,点D在线段BC上,且△ABC∽△DBA,则下列结论一定正确的是( )| A. | AB2=BC•BD | B. | AB2=AC•BD | C. | AB•AD=BD•BC | D. | AB•AC=BC•BD |
 如图是一无盖的正方体盒子,下列展开图不能叠合成无盖正方体的是( )
如图是一无盖的正方体盒子,下列展开图不能叠合成无盖正方体的是( )



 图①为三角形纸片ABC,AB上有一点P,已知将A、B、C往内折至P时,出现折线SR、TQ、RQ,其中Q、R、S、T四点分别在BC、AC、AP、BP上,如图②所示,若△ABC、四边形PTQR的面积分别为16、5,则△RPS面积为3.
图①为三角形纸片ABC,AB上有一点P,已知将A、B、C往内折至P时,出现折线SR、TQ、RQ,其中Q、R、S、T四点分别在BC、AC、AP、BP上,如图②所示,若△ABC、四边形PTQR的面积分别为16、5,则△RPS面积为3.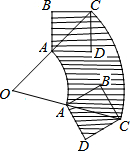 如图所示,正方形ABCD对角线AC所在直线上有一点O,OA=AC=2,将正方形绕O点顺时针旋转60°,则图中阴影部分的面积是2π+2.
如图所示,正方形ABCD对角线AC所在直线上有一点O,OA=AC=2,将正方形绕O点顺时针旋转60°,则图中阴影部分的面积是2π+2.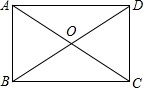 如图所示,矩形ABCD中,对角线AC、BD相交于O,∠ADB=30°,BD=6cm,试求此矩形的周长和面积.
如图所示,矩形ABCD中,对角线AC、BD相交于O,∠ADB=30°,BD=6cm,试求此矩形的周长和面积.