题目内容
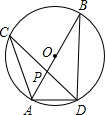 如图,在⊙O中,直径AB与弦CD相交于点P,∠CAB=40°,∠APD=70°.
如图,在⊙O中,直径AB与弦CD相交于点P,∠CAB=40°,∠APD=70°.(1)求∠B的大小;
(2)已知AD=4cm,求弧AD的长.
考点:圆周角定理,弧长的计算
专题:计算题
分析:(1)先利用三角形外角性质得∠APD=∠PDB+∠B,再根据圆周角定理得∠PDB=∠CAB=40°,然后利用∠B=∠APD-∠CAB进行计算;
(2)连结OD,如图,根据圆周角定理得∠AOD=2∠B=60°,则可判断△OAD为等边三角形,则OA=AD=4cm,然后根据弧长公式求解.
(2)连结OD,如图,根据圆周角定理得∠AOD=2∠B=60°,则可判断△OAD为等边三角形,则OA=AD=4cm,然后根据弧长公式求解.
解答:解:(1)∵∠APD=∠PDB+∠B,
而∠PDB=∠CAB=40°,
∴∠B=70°-40°=30°;
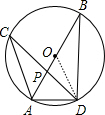 (2)连结OD,如图,
(2)连结OD,如图,
∵∠AOD=2∠B,
而∠B=30°,
∴∠AOD=60°,
∴△OAD为等边三角形,
∴OA=AD=4cm,
∴弧AD的长=
=
π(cm).
而∠PDB=∠CAB=40°,
∴∠B=70°-40°=30°;
 (2)连结OD,如图,
(2)连结OD,如图,∵∠AOD=2∠B,
而∠B=30°,
∴∠AOD=60°,
∴△OAD为等边三角形,
∴OA=AD=4cm,
∴弧AD的长=
| 60•π•4 |
| 180 |
| 4 |
| 3 |
点评:本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.推论:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.也考查了弧长公式.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
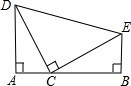 已知:如图,在△CDE中,∠DCE=90°,CD=CE,直线AB经过点C,且点D、E在直线AB的同侧,在直线AB上点C的左、右两侧分别取点A、B,使得∠DAC=∠EBC=∠DCE.
已知:如图,在△CDE中,∠DCE=90°,CD=CE,直线AB经过点C,且点D、E在直线AB的同侧,在直线AB上点C的左、右两侧分别取点A、B,使得∠DAC=∠EBC=∠DCE. 如图是一张等边三角形网格纸片,现要沿着一条经过点A的格线把它剪成两个形状大小相同的纸片,求不同裁减方案(若两次能重叠,则只算一种).
如图是一张等边三角形网格纸片,现要沿着一条经过点A的格线把它剪成两个形状大小相同的纸片,求不同裁减方案(若两次能重叠,则只算一种).