题目内容
已知二次函数y=x2+bx-3的图象经过点P(-2,5),求b的值,并写出当1<x≤3时y的取值范围.
考点:二次函数图象上点的坐标特征,二次函数的性质
专题:
分析:求出函数与x轴的交点和函数的最小值点是解题的关键.
解答:解:将点P(-2,5)代入y=x2+bx-3得,
4-2b-3=5,
b=-2,
原式可化为y=x2-2x-3,
当y=0时,x2-2x-3=0,
(x+1)(x-3)=0,
x1=-1,x2=3,
其对称轴为x=-
=1,最小值为y=-4,
∴1<x≤3时,-4<y≤0.
4-2b-3=5,
b=-2,
原式可化为y=x2-2x-3,
当y=0时,x2-2x-3=0,
(x+1)(x-3)=0,
x1=-1,x2=3,
其对称轴为x=-
| -2 |
| 2×1 |
∴1<x≤3时,-4<y≤0.
点评:本题考查了二次函数的性质和二次函数图象上点的坐标特征,要熟悉函数和方程的关系.

练习册系列答案
相关题目
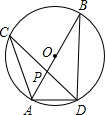 如图,在⊙O中,直径AB与弦CD相交于点P,∠CAB=40°,∠APD=70°.
如图,在⊙O中,直径AB与弦CD相交于点P,∠CAB=40°,∠APD=70°. 如图,△ABC的高BD,CE相交于点F.
如图,△ABC的高BD,CE相交于点F. 如图,△ABC为等边三角形,点D是BC边上异于B,C的任意一点,DE⊥AB于点E,DF⊥AC于点F.若BC边上的高线AM=2,则DE+DF=
如图,△ABC为等边三角形,点D是BC边上异于B,C的任意一点,DE⊥AB于点E,DF⊥AC于点F.若BC边上的高线AM=2,则DE+DF=