题目内容
 如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.求证:E是BF的中点.
如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.求证:E是BF的中点.考点:全等三角形的判定与性质
专题:证明题
分析:由AF与BC平行,利用两直线平行得到两对内错角相等,再由E为AD中点,得到AE=DE,利用AAS得到三角形AEF与三角形DEB全等,利用全等三角形对应边相等得到EF=BF,即E为BF的中点.
解答:证明:∵AF∥BC,
∴∠AFB=∠FBD,∠FEA=∠BED,
∵E为AD的中点,
∴EA=ED,
在△FEA和△BED中,
,
∴△FEA≌△BED(AAS),
∴FE=BE,即E是BF的中点.
∴∠AFB=∠FBD,∠FEA=∠BED,
∵E为AD的中点,
∴EA=ED,
在△FEA和△BED中,
|
∴△FEA≌△BED(AAS),
∴FE=BE,即E是BF的中点.
点评:此题考查了全等三角形的判定与性质,平行线的判定与性质,熟练掌握全等三角形的判定与性质是解本题的关键.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
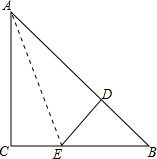 已知Rt△ABC中,∠ACB=90°,AC=BC,AD=AC,DE⊥AB,垂足为D,交BC于点E.求证:BD=DE=CE.
已知Rt△ABC中,∠ACB=90°,AC=BC,AD=AC,DE⊥AB,垂足为D,交BC于点E.求证:BD=DE=CE.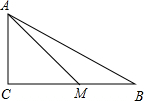 已知在△ABC中,∠C=90°,M在BC上,若AB=17,AM=10,BM=9,求AC、MC的长.
已知在△ABC中,∠C=90°,M在BC上,若AB=17,AM=10,BM=9,求AC、MC的长.